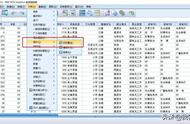
旋转前后的因子载荷矩阵,给出了旋转前后的因子载荷矩阵,其中“成分矩阵”表是初始的未经旋转的载荷矩阵,“旋转成分矩阵”是经过旋转后的载荷矩阵。一般情况下,经过因子旋转后变量在因子上的载荷分布更加分散,因而比未旋转时容易解释。

因子得分的系数矩阵。输出的是因子得分系数矩阵。对于每个因子,把系数和对应的课程名称相乘后再求和,可以得到最终的因子得分公式,利用它就能够对所有案例进行因子评分了。
例如,因子1的得分公式为:FAC1_1=-0.152*无机一0.065*哲学 0.232*思品一0.054*高数I ... 0.121*微生物 0.069*天然药化-0.040*专业英语-0.154*药理学。
综合评分如果要关心的是学生的综合能力,可对8个公因子的得分进行加权求和,权数就取其方差贡献值或方差贡献率,参看图22-13中“旋转平方和载入”一栏里的“合计”(方差值)、“方差的%”(方差贡献率)。本例采用方差贡献率作为加权变量,8个旋转后公因子的方差贡献率依次为:13.3%、12.18%、9.71%、9.3%、8.78%、6.74%、4.77%、3.79%。
由此可得学生的综合得分计算公式如下:
ZF=13.30%*FAC1_1 12.18%*FAC2_1 9.71%*FAC3_1 9.30%*FAC4_1 8.78%*FAC5_1 6.74%*FA C6_1 4.77%*FAC7_1 3.79%*FAC8_1,其中FACn_1表示第n个因子的得分。
通过前面的分析,利用因子得分系数和方差贡献率已经得到了能够进行综合评分的公式,由此可以对学生成绩进行更为科学的判断和排序。