在阅读此文之前,希望用您发财的小手点一下“关注”,文章内容来源于网络但是最后会有小编的个人感悟,如有不足之处可以评论指出,谢谢您的支持。
无理数与数学中的无限之美
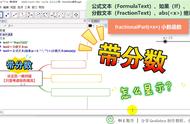
数学是一门充满无限之美的学科,其中包含了许多令人惊奇的数。在数学的世界里,有理数和整数是我们最为熟悉的数,它们可以用两个整数的比来表示,例如2/3或者5。然而,数学的宇宙中还有一类特殊的数字,被称为无理数(irrational number),它们无法表示为两个整数之比。这些神秘的数字令人着迷,因为它们蕴含着无穷的奥秘。

无理数的特性
无理数有一个明显的特点,那就是无法表示为有理数的形式。有理数包括整数和分数,而无理数则无法被精确表示为这两者之一。最著名的无理数之一就是圆周率π(pi),它的小数部分永不重复,也永不终止,这是一个无限不循环小数。

虽然无理数无法被精确表示为有理数,但有趣的是,有些无理数可以通过基本的数学运算变成有理数或整数。例如,如果你将两个无理数相加,它们的和可能是一个有理数。然而,有一个特殊的无理数,无论如何努力,都不可能变成整数或有理数,这使它成为数学中的一道难题。

一个特殊的无理数
这个特殊的无理数由三个无理数的组合构成,它的计算公式非常复杂,即便使用计算机也很难得到其准确值。这个无理数被称为"难以捉摸的数",因为它无法被一般的数学运算精确表示。在数学领域,这类数字被称为超越数(transcendental number),它们是一类极为特殊的无理数。