极坐标两点间的距离公式,极坐标的两点间的距离公式

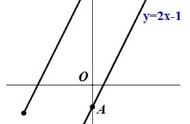
极坐标的两点间的距离公式

我们可以通过回顾距离公式来求极坐标之间的距离。 当我们想求两个极坐标之间的距离时，知道这个技巧会很有用，我们不想把它们转换成它们的直角形式。

我们可以用极坐标的半径和参数来求极坐标之间的距离。

这篇文章将展示我们如何推导极坐标的距离公式，并学习如何在不同的例子和问题中应用它。 在我们这样做之前，请务必回顾一下以下内容:

• 确保理解在直角坐标系中应用的距离公式。
• 复习极坐标表达式的知识，并将矩形表达式转换为极坐标表达式。
• 复习一下以前学过的最常见的三角恒等式。

让我们继续，深入到公式和计算两个极坐标之间距离的过程中。

要理解如何将距离公式应用于极坐标，最好的方法是从直角坐标的距离公式推导出。

这是一个形象化的两个极坐标如何在xy坐标系中。 回忆一下两点(x1,y1)和(x2,y2)之间的距离，等于

因为极坐标与直角坐标关系如下图：

可以将这两点表示为两个极坐标(r1cosθ1,r1sinθ1)和(r2cosθ1,r2sinθ1)。 我们可以用极坐标的半径和辐角来重写距离公式。