1
专题七 坐标系与参数方程二轮复习学案
1.(2019·高考全国卷Ⅲ)如图,在极坐标系 Ox中,A(2,0),B2,π
4 ,C2,3π
4 ,D(2,
π),弧AB︵
,BC︵
,CD︵
所在圆的圆心分别是(1,0),1,π
2 ,(1,π),曲线 M1是弧AB︵
,曲线
M2是弧BC︵
,曲线 M3是弧CD︵
.
(1)分别写出 M1,M2,M3的极坐标方程;
(2)曲线 M由 M1,M2,M3构成,若点 P在 M上,且|OP|= 3,求 P的极坐标.
2.(2019·高考全国卷Ⅰ)在直角坐标系 xOy中,曲线 C的参数方程为
x=1-t2
1+t2,
y= 4t1+t2
(t为参
数).以坐标原点 O为极点,x轴的正半轴为极轴建立极坐标系,直线 l的极坐标方程为 2ρcos
θ+ 3ρsin θ+11=0.
(1)求 C和 l的直角坐标方程;
(2)求 C上的点到 l距离的最小值.
2
1.坐标系与参数方程是高考的选考内容之一,高考考查的重点主要有两个方面:一是
简单曲线的极坐标方程;二是参数方程、极坐标方程与曲线的综合应用.
2.全国卷对此部分内容的考查以解答题形式出现,难度中等,备考此部分内容时应注
意转化思想的应用.
极坐标方程及其应用
[典型例题]
(2019·高考全国卷Ⅱ)在极坐标系中,O为极点,点 M(ρ0,θ0)(ρ0>0)在曲线 C:ρ
=4sin θ上,直线 l过点 A(4,0)且与 OM垂直,垂足为 P.
(1)当θ0=π3时,求ρ0及 l的极坐标方程;
(2)当 M在 C上运动且 P在线段 OM上时,求 P点轨迹的极坐标方程.
[对点训练]
1.(2019·合肥模拟)在直角坐标系 xOy中,直线 l1:x=0,圆 C:(x-1)2+(y-1- 2)2
=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(1)求直线 l1和圆 C的极坐标方程;
(2)若直线 l2的极坐标方程为θ=π4(ρ∈R),设 l1,l2与圆 C的公共点分别为 A,B,求△OAB
的面积.
3
2.(2018·高考全国卷Ⅰ)在直角坐标系 xOy中,曲线 C1的方程为 y=k|x|+2.以坐标原点
为极点,x轴正半轴为极轴建立极坐标系,曲线 C2的极坐标方程为ρ2+2ρcos θ-3=0.
(1)求 C2的直角坐标方程;
(2)若 C1与 C2有且仅有三个公共点,求 C1的方程.
参数方程及其应用
[典型例题]
(2018·高考全国卷Ⅱ)在直角坐标系 xOy中,曲线 C的参数方程为x=2cos θ,
y=4sin θ(θ
为参数),直线 l的参数方程为x=1+tcos α,
y=2+tsin α(t为参数).
(1)求 C和 l的直角坐标方程;
(2)若曲线 C截直线 l所得线段的中点坐标为(1,2),求 l的斜率.
4
[对点训练]
1.已知曲线 C:x2
4+y2
9=1,直线 l:
x=2+t,
y=2-2t(t为参数).
(1)写出曲线 C的参数方程,直线 l的普通方程;
(2)过曲线 C上任意一点 P作与 l夹角为 30°的直线,交 l于点 A,求|PA|的最大值与最小
值.
2.在直角坐标系 xOy中,曲线 C的参数方程为x=4cos θ
y=2sin θ(θ为参数),直线 l的参数方
程为x=t+ 3,
y=2t-2 3(t为参数),直线 l与曲线 C交于 A,B两点.
(1)求|AB|的值;
(2)若 F为曲线 C的左焦点,求FA→·FB→的值.
5
极坐标方程与参数方程的综合应用
[典型例题]
(2019·福建省质量检查 )在平面直角坐标系 xOy 中,直线 l 的参数方程为
x=1+35t,
y=1+45t
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线 C的
极坐标方程为ρ2= 21+sin2θ
,点 P的极坐标为( 2,π4).
(1)求 C的直角坐标方程和 P的直角坐标;
(2)(一题多解)设 l与 C交于 A,B两点,线段 AB的中点为 M,求|PM|.
[对点训练]
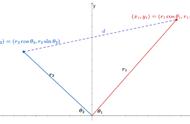
1. (2019·石家庄市模拟 (一 ))在平面直角坐标系 xOy 中,曲线 C 的参数方程为
x=rcos α+2
y=rsin α(α为参数),以坐标原点 O为极点,x轴的正半轴为极轴建立极坐标系,射线 l
的极坐标方程为θ=π3.
(1)求曲线 C的极坐标方程;
(2)当 0<r<2时,若曲线 C与射线 l交于 A,B两点,求 1|OA|
+1
|OB|的取值范围.
6
2.(2019·江西八所重点中学联考)在平面直角坐标系 xOy中,以坐标原点 O为极点,x
轴的正半轴为极轴建立极坐标系,曲线 M的极坐标方程为ρ=2cos θ,若极坐标系内
异于 O的三点 A(ρ1,φ),B(ρ2,φ+π6),C(ρ3,φ-
π6)(ρ1,ρ2,ρ3>0)都在曲线 M上.
(1)求证: 3ρ1=ρ2+ρ3;
(2)若过 B,C两点的直线的参数方程为
x=2- 32t
y=12t
(t为参数),求四边形 OBAC的面积.
1.(2019·东北四市联合体模拟(一))在平面直角坐标系 xOy中,直线 l1的倾斜角为 30°,
且经过点 A(2,1).以坐标原点 O为极点,x轴正半轴为极轴建立极坐标系,直线 l2:ρcos θ
=3.从坐标原点 O作射线交 l2于点 M,点 N为射线 OM上的点,满足|OM|·|ON|=12,记点
N的轨迹为曲线 C.
(1)写出直线 l1的参数方程和曲线 C的直角坐标方程;
(2)设直线 l1与曲线 C交于 P,Q两点,求|AP|·|AQ|的值.
7
2.(2019·四省八校双教研联考)在平面直角坐标系 xOy中,曲线C1的参数方程为x=2t
y=t2(其
中 t为参数).以坐标原点 O为极点,x轴正半轴为极轴建立极坐标系,并取相同的单位长度,
曲线 C2的极坐标方程为ρcos(θ+π3)=1.
(1)求曲线 C1的普通方程和 C2的直角坐标方程;
(2)过 P(0,1)的直线 l交曲线 C1于 A,B两点,当|PA|·|PB|=8时,求直线 l的倾斜角.
3.(2019·广州市综合检测(一))在平面直角坐标系 xOy中,曲线C1的参数方程为x=cos t
y=sin2t(t
为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线 C2的极坐标方程为
ρ(sin θ-acos θ)=12(a∈R).
(1)写出曲线 C1的普通方程和直线 C2的直角坐标方程;
(2)若直线 C2与曲线 C1有两个不同的交点,求 a的取值范围.
8
4. (2019·湖南省湘东六校联考 )在平面直角坐标系 xOy 中,直线 l 的参数方程为
x=7-t,
y=-2+t(t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线 C:ρ
=4 2sin(θ+π4).
(1)求直线 l的普通方程和曲线 C的直角坐标方程;
(2)设曲线 C与直线 l的交点为 A,B,Q是曲线 C上的动点,求△ABQ面积的最大值.
5.(2019·济南市学习质量评估)在平面直角坐标系 xOy中,以坐标原点 O为极点,x轴
的正半轴为极轴建立极坐标系,曲线 C的极坐标方程为ρcos2θ=sin θ,直线 l的参数方程为
x= 32t
y=a+12t(t为参数,其中 a>0),直线 l与曲线 C相交于 M,N两点.
(1)求曲线 C的直角坐标方程;
(2)若点 P(0,a)满足 1|PM|
+1
|PN|=4,求 a的值.
9
6.(2019·广东省七校联考)在平面直角坐标系 xOy中,曲线 C1:x=a+acos φ,
y=asin φ(φ为参
数,实数 a>0),曲线 C2:x=bcos φ,
y=b+bsin φ(φ为参数,实数 b>0).在以坐标原点 O为极点,x
轴的正半轴为极轴的极坐标系中,射线 l:θ=α(ρ≥0,0≤α≤π2)与 C1交于 O,A两点,与
C2交于 O,B两点,当α=0时,|OA|=1;当α=π2时,|OB|=2.
(1)求 a,b的值;
(2)求 2|OA|2+|OA|·|OB|的最大值.
7.(2019·合肥市第一次质量检测)已知曲线 C的参数方程为x= 10
2cos α
y=sin α(α为参数),以
平面直角坐标系的原点 O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线 C的极坐标方程;
(2)P,Q为曲线 C上两点,若OP→ ·OQ→=0,求|OP→ |2·|OQ→ |2
|OP→ |2+|OQ→ |2的值.
10
8.(2019·郑州市第二次质量预测)在平面直角坐标系 xOy中,以 O为极点,x轴的正半
轴为极轴,建立极坐标系,曲线 C的极坐标方程为ρ2cos2θ+3ρ2sin2θ=12,直线 l的参数方
程为
x=-2+ 22t
y= 22t
(t为参数),直线 l与曲线 C交于 M,N两点.
(1)若点 P的极坐标为(2,π),求|PM|·|PN|的值;
(2)求曲线 C的内接矩形周长的最大值.
11
1.(2019·东北四市联合体模拟(一))在平面直角坐标系 xOy中,直线 l1的倾斜角为 30°,
且经过点 A(2,1).以坐标原点 O为极点,x轴正半轴为极轴建立极坐标系,直线 l2:ρcos θ
=3.从坐标原点 O作射线交 l2于点 M,点 N为射线 OM上的点,满足|OM|·|ON|=12,记点
N的轨迹为曲线 C.
(1)写出直线 l1的参数方程和曲线 C的直角坐标方程;
(2)设直线 l1与曲线 C交于 P,Q两点,求|AP|·|AQ|的值.
2.(2019·四省八校双教研联考)在平面直角坐标系 xOy中,曲线C1的参数方程为x=2t
y=t2(其
中 t为参数).以坐标原点 O为极点,x轴正半轴为极轴建立极坐标系,并取相同的单位长度,
曲线 C2的极坐标方程为ρcos(θ+π3)=1.
(1)求曲线 C1的普通方程和 C2的直角坐标方程;
(2)过 P(0,1)的直线 l交曲线 C1于 A,B两点,当|PA|·|PB|=8时,求直线 l的倾斜角.
12
3.(2019·广州市综合检测(一))在平面直角坐标系 xOy中,曲线 C1的参数方程为x=cos t
y=sin2t(t
为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线 C2的极坐标方程为
ρ(sin θ-acos θ)=12(a∈R).
(1)写出曲线 C1的普通方程和直线 C2的直角坐标方程;
(2)若直线 C2与曲线 C1有两个不同的交点,求 a的取值范围.
4. (2019·湖南省湘东六校联考 )在平面直角坐标系 xOy 中,直线 l 的参数方程为
x=7-t,
y=-2+t(t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线 C:ρ
=4 2sin(θ+π4).
(1)求直线 l的普通方程和曲线 C的直角坐标方程;
(2)设曲线 C与直线 l的交点为 A,B,Q是曲线 C上的动点,求△ABQ面积的最大值.
13
5.(2019·济南市学习质量评估)在平面直角坐标系 xOy中,以坐标原点 O为极点,x轴
的正半轴为极轴建立极坐标系,曲线 C的极坐标方程为ρcos2θ=sin θ,直线 l的参数方程为
x= 32t
y=a+12t(t为参数,其中 a>0),直线 l与曲线 C相交于 M,N两点.
(1)求曲线 C的直角坐标方程;
(2)若点 P(0,a)满足 1|PM|
+1
|PN|=4,求 a的值.
6.(2019·广东省七校联考)在平面直角坐标系 xOy中,曲线 C1:x=a+acos φ,
y=asin φ(φ为参
数,实数 a>0),曲线 C2:x=bcos φ,
y=b+bsin φ(φ为参数,实数 b>0).在以坐标原点 O为极点,x
轴的正半轴为极轴的极坐标系中,射线 l:θ=α(ρ≥0,0≤α≤π2)与 C1交于 O,A两点,与
C2交于 O,B两点,当α=0时,|OA|=1;当α=π2时,|OB|=2.
(1)求 a,b的值;
(2)求 2|OA|2+|OA|·|OB|的最大值.
14
7.(2019·合肥市第一次质量检测)已知曲线 C的参数方程为x= 10
2cos α
y=sin α(α为参数),以
平面直角坐标系的原点 O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线 C的极坐标方程;
(2)P,Q为曲线 C上两点,若OP→ ·OQ→=0,求|OP→ |2·|OQ→ |2
|OP→ |2+|OQ→ |2的值.
8.(2019·郑州市第二次质量预测)在平面直角坐标系 xOy中,以 O为极点,x轴的正半
轴为极轴,建立极坐标系,曲线 C的极坐标方程为ρ2cos2θ+3ρ2sin2θ=12,直线 l的参数方
程为
x=-2+ 22t
y= 22t
(t为参数),直线 l与曲线 C交于 M,N两点.
(1)若点 P的极坐标为(2,π),求|PM|·|PN|的值;
(2)求曲线 C的内接矩形周长的最大值.
,