总之,μ决定了正态分布的位置,与μ越近,被取到的概率就越大,反之越小。σ描述的是正态分布的离散程度。σ越大,数据分布越分散曲线越扁平;σ越小,数据分布越集中曲线越陡峭。
下图是从网上找的σ=0.5,σ=1,σ=2 三条曲线的对比:

简单来说,标准差是一组数据平均值分散程度的一种度量。一个较大的标准差,代表大部分数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。

在一个正态分布中,有 68.2% 的点落在 ±1 个标准差的范围内,约有 95.5% 的点落在 ±2 个标准差的范围内,约有 99.7% 的点落在 ±3 个标准差的范围内。这个叫做三西格玛准则。
三、工资分配的逻辑
工资分配的数学计算过程,一个企业1000名员工,老板能够付出多少工资很容易计算出来,平均每人工资10000元×1000人=1000万元。
这1000名员工中,如何区别对待呢?平均分配会导致企业没有活力,大家消极怠工。然而工作能力优秀的占少数,差的占少数,大多数人一般般,符合正态分布,N(μ,σ2)中,μ为均数取值10000,σ为标准差,如果取值到小,也就是大部分人的工资与10000的差距太小,如果取值太大,工资差距就变大。
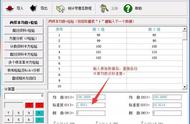
我们用EXCEL表形象的推导一下,假设该公司以500元为一档,从2000元起,最高15500,μ=10000,σ=1000或者σ=500,使用正态分布记录他们出现的概率。使用到的函数就是
NORMDIST((2000-15500),10000,500,FALSE)
EXCEL表自带的函数,你不用纠结复杂度,套用就行,得出下图:

中间突起的就是10000,很多员工的工资都在这个值附近,当工资与平均工资的标准差1000时,曲线就比较平,很多人分布在不同的工资区域,当工资与平均工资的标准差500,曲线就比较陡,很多人工资集中在10000附近。
结合三西格玛准则,一个员工工资达到15500的概率,已经是小数点后面的第9位,这种人可以叫做人中龙凤。
工资的平均,让企业失去了活力甚至崩溃;工资差距的拉大,失去某种公平性。也导致人中龙凤过多而不再是龙凤,从而优秀员工流失率太高,流失了优秀,又重新回到工资的平均。而左右以上两种局面就是标准差,我把它称为参数一。
那么,让企业失去了活力甚至崩溃的参数是什么呢?我从区块链技术的共识机制找到了答案。
四、拜占庭将军问题
话说很久很久以前,有一个叫拜占庭的帝国,派出了6路大军攻打一个小国,每个将军率领1路大军,但这个小国也很是厉害,需要4路大军同时发动进攻才能攻下,任何1路大军单独攻击都会被小国打残。这6路大军之间都是通过通信兵来相互协商是否攻击以及时间的时间,这些将军里面可能是有叛徒,叛徒可能撒谎,约定进攻时不进攻。在这种状态下,拜占庭将军们怎样才能保证有多于4支军队在同一时间一起发起进攻,从而赢得战争?
图灵奖得主莱斯利·兰伯特(Leslie Lamport)采用递归算法,给了我们一个结论公式。全部将军数大于3倍叛徒将军数。
设叛徒将军数为M,那么能够一起达成共识一起进攻,即:M<总人数/3。
论证过程过于复杂,在莱斯利·兰伯特1982年发表的论文中,我看不明白,只记得结论。
那么一个企业,工资太平均,导致有些人消极怠工(或者说阳奉阴违),这种人的人数达到多少,就导致企业失去活力甚至崩盘呢,拜占庭将军问题和兰伯特的结论公式给了我们类比的答案。
M<总人数/3 我把它称为参数二。
上述公司中,由于参数一设置问题,导致工资过于平均,频率崩盘,那么消极怠工人数按照参数二,可得不超过3333人,接着要乘以一倍标准差的概率68.2%,最终结果是不超过2266人。
五、思想结论
感谢大家看我胡扯这么多,在人力资源管理工资分配的问题上,其实没有终极解决方案,只不过冥思苦想了很久,推导出了所谓的基于数学理论知识的参数一和参数二。
我猜想,一个优秀管理者,
一定是能够敏锐地判断出参数二的临界点,
从而快速对参数一进行调整,
至于调整多少,没有标准答案,这个是艺术。