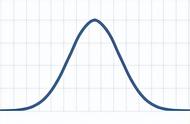
平均值(Mean)、中位数(Median)和标准差(Standard Deviation)是常用的统计量,它们都用来描述数据的集中趋势和离散程度。它们的特点和适用场景如下:
平均值:特点:平均值是一组数据的总和除以数据的个数,用于表示数据的集中趋势。它具有良好的数学性质,计算简便,容易理解和解释。适用场景:适用于数据分布近似对称的情况,且异常值的影响不大的情况。比如身高、体重等连续型数据。
中位数:特点:中位数是一组数据中居于中间位置的数值,用于表示数据的集中趋势。它不受极端值的影响,更加稳健。适用场景:适用于数据分布较为偏态或存在异常值的情况,可以更准确地反映数据的中心位置。比如收入、财富等数据。
标准差:特点:标准差是一组数据偏离平均值的程度,用于表示数据的离散程度。标准差越大,数据的分布越分散。适用场景:适用于数据分布近似正态分布的情况,能够反映数据的离散程度。比如成绩、生产效率等数据。
需要注意的是,在实际应用中,平均值、中位数、标准差等统计量的选择应该根据具体问题的性质和数据的特点来进行,不能一概而论。同时,在计算这些统计量时,也需要考虑数据的有效性、异常值的处理等问题。
,