甘肃2023统招专升本考试内容整理—制图基本知识关于直线的其他投影特性。考点整理如下,希望对大家有所帮助。
(一)直线上点的投影
1、直线上点的投影
点在直线上,则点的各个投影必定在该直线的同面投影上,反之,若一个点的各个投影都在直线的同面投影上,则该点必定在直线上。
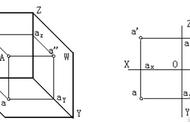
举例:所示直线AB上有一点C,则C点的三面投影c、c′、c″ 必定分别在该直线AB的同面投影ab、a′ b′、a″b″ 上。

直线上点的投影
2、直线投影的定比性
直线上的点分割线段之比等于其投影之比,这称为直线投影的定比性。
点C在线段AB上,它把线段AB分成AC和CB两段。根据直线投影的定比性,AC:CB = ac:cb = a′ c′:c′ b′ = a″c″:c″b″ 。

直线投影的定比性
(二)两直线的相对位置
两直线的相对位置有平行、相交、交叉三种情况。
1、两直线平行
(1)特性
若空间两直线平行,则它们的各同面投影必定互相平行。由于AB∥CD,则必定ab∥cd、 a′ b′∥c′ d′、a″b″∥c″d″ 。反之,若两直线的各同面投影互相平行,则此两直线在空间也必定互相平行。

两直线平行
(2)判定两直线是否平行
1)如果两直线处于一般位置时,则只需观察两直线中的任何两组同面投影是否互相平行即可判定。
2)当两平行直线平行于某一投影面时,则需观察两直线在所平行的那个投影面上的投影是否互相平行才能确定。两直线AB、CD均为侧平线,虽然ab∥cd、 a′b′∥c′d′,但不能断言两直线平行,还必需求作两直线的侧面投影进行判定,两直线的侧面投影a″b″ 与c″d″相交,所以可判定直线AB、CD不平行。