统计学图表中r平方怎么算,统计学中r平方和r的关系

R2是一种易于计算和非常直观的用于度量相关性的指标

我们中的大多数人已经熟悉了相关性和它的度量标准R，就是常说的Pearson相关系数。

如果相关系数R接近1或者-1，则说明这两个变量是密切相关的, 比如身高与体重。

其实R平方和R非常相似，但是R平方在理解上更容易。

例如：实际上当R=0.7时比0.5要好2倍，但是在数值上面并不直观。R2可以直接反映出R2=0.7优于R2=0.5的1.4倍。

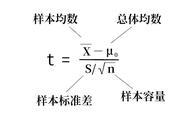
R方一般用在回归模型用用于评估预测值和实际值的符合程度，R方的定义如下：变量x引起y变异的回归平方和占y变异总平方和的比率，也称为拟合优度
表达式：R2=SSR/SST=1-SSE/SST
决定系数反应了y的波动有多少百分比能被x的波动所描述，即表征依变数Y的变异中有多少百分比,可由控制的自变数X来解释.

举一个例子：我们用小鼠大小为X轴，Y轴代表小鼠体重, Y坐标越高代表小鼠体重越大。

在这里, 我们将平均值画成一条黑线，同时再根据数据拟合一条直线（蓝线）。

假设我们知道单个小鼠的大小，那么小鼠体重预测的最佳方法是用什么呢？

我们刚才画的蓝线是否比平均线能更好地解释数据？

如果是的话, 好了多少？

直观来看，看起来蓝线比平均值更好地贴合数据。我们如何量化这两条线的差异？

R2！！

image.png

下图是R2的计算公式：

方程中Var(mean)是数据与平均值相关的差异，实际数据值与其平均值的差的平方和

方程中Var(line)是蓝线与数据点之间的差异，实际数据值与蓝线对应点的数值差的平方和

所以, 这使得R2的值的范围是从0到1。

image.png

现在我们将通过一个例子来一步一步计算一下R2：

image.png

实际数据值与蓝线对应点的数值差的平方和等于6

image.png

根据公式，我们可以计算得到R2=0.81=81%

image.png

这意味着蓝线与数据点的差值平方和Var(line) 比 均值Var(mean)的对应数值 少81%

也就是说, 小鼠的大小与重量的相关性能够解释总差异的81%，这意味着数据的大部分变化都可以由小鼠重量-大小的关系来解释。

再举另一个示例，我们比较两个可能不相关的变量：

Y轴依然是小鼠重量

X轴表示小鼠嗅探一块岩石的时间

image.png

与之前的计算一致, 得到Var(mean) = 32

然而, 我们计算蓝线与数据点差的平方和Var(line)时，得到了一个很大的值, 30

通过计算, 我们看到 R2= 0.06 = 6%

因此, 新拟合的线只比平均值多解释了6%的差异，也就是说, X与Y二者的相关性仅能解释总差异的6%

当有人说这个统计学计算R2 =0.9，你可以认为这两个变量之间的相关性非常好。数据变化的90%可以被解释。

R2 就是相关系数R的平方，当有人说统计显著的R = 0.9时，R2 =0.81，这两个变量解释了81%的数据与拟合直线间的差异。

同样，比较R=0.7与R=0.5哪个要好得多，如果我们把这些数字转换成R平方：

当R = 0.7时, R2 ≈0.5

当R=0.5时，R2 =0.25

用R平方很容易看出, 第一个相关性是第二个相关性的2倍！！

需要注意的是, R平方并不能表示相关性的方向（因为平方数不会小于0）。