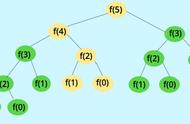
分享一个隐藏着宇宙中的某个终极奥秘的神秘数列——斐波那契数列!
指的是这样一个数列:1、1、2、3、5、8、13、21、34、55、89、144……
数列中的每一项称为斐波那契数,从第3项开始,每1项都等于前两项之和。
在数学上,斐波那契数列以如下被以递推的方法定义:
F(1)=1,
F(2)=1,
F(n)=F(n - 1) F(n - 2)(n ≥ 3,n ∈ N*)
斐波那契弧线,也称为斐波那契扇形线。

斐波那契弧线:
第一,此趋势线以二个端点为准而画出,例如,最低点反向到最高点线上的两个点。然后通过第二点画出一条“无形的(看不见的)”垂直线。然后,从第一个点画出第三条趋势线:38.2%, 50%和61.8%的无形垂直线交叉。
斐波纳契弧线,是潜在的支持点和阻力点水平价格。斐波纳契弧线和斐波纳契扇形线常常在图表里同时绘画出。支持点和阻力点就是由这些线的交汇点得出。
与黄金分割的关系
有趣的是,这样一个完全是自然数的数列,通项公式却是用无理数来表达的。
通项公式:

而且当趋向于无穷大时,前一项与后一项的比值越来越逼近黄金分割0.618(或者说后一项与前一项的比值小数部分越来越逼近 0.618)。