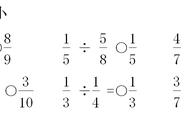1.出示例题
“把4个同样大的橙子分给小朋友。如果每人吃2个,可以分给几人?”
学生列式算出结果。4÷2=2(人)
继续提问:如果每人吃1个,可以分给几人?
学生列式算出结果。4÷1=4(人)
请同学们思考,为什么刚刚的两个问题都要用除法来计算?
(明确:第一问是在求4里面有几个2,第二问是在求4里面有几个1,所以都用除法计算。)
2.变式问题
过渡:老师将题目改动一下,变成“每人吃1/2个,可以分给几人?”现在又该如何列算式?
列式:4÷1/2=
提问:这个问题为什么也用除法计算?
(其实就是求4里面有几个1/2,所以也用除法计算)
师:请大家观察这道算式,这里的被除数是(整数),除数是(分数),今天我们就一起来研究整数除以分数。(板书课题)
提出:你知道这道算式的结果是多少吗?为什么是8?你有什么办法来证明?和同桌交流你的想法。
预设1:用小数来表示。4÷0.5=8
师评价:这个方法也是可以的,不过我们知道有些分数无法化成有限小数,所以这种方法有局限性,我们暂不展开研究。
预设2:学生画图表示。贴出4个橙子图。一个橙子可以分给2人,4个橙子就分给4个2人,就是8人。4个2人,算式就是4×2。
提问:这里的2表示什么意思?(2表示1个橙子可以平均分给2个小朋友)
师小结:看样子用画图来解答这道题目是一种很棒的方法,让人看得清楚、明白。
3.初建模型
师:如果每人吃1/4个呢,可以分给几人?可以怎样列示?(4÷1/4)
引导:4÷1/4该怎样计算呢?请同学们独立完成导学单第1题,先画一画,再算一算,完成后与同桌交流你的想法。
指名学生上黑板画图分析。(先画4个圆,代表4个橙子。将其中的一个橙子平均分成4份,4个橙子就被分成了16份。)
怎样用算式表示刚才的图意?
板书:4÷1/4=4×4=16(人)
问:这里的4表示什么意思?(1个橙子可以平均分给4个小朋友)
三、教学例3 (整数除以几分之几)

1.应用模型
出示图文:“4米长的彩带,每1/3米剪一段,可以剪成多少段?”
读题,说出数量关系式并列式。
生1:总米数÷每段的米数=段数
生2:4÷1/3
师:如果用画图来表示4÷1/3的结果,我们可以怎么画呢?
(先画4米,顺次标出所有的1/3米)
生:一个1/3米为一段,1米中有3段,4米中有4个3段,所以是4×3。
师:我们将4÷1/3转化成了4×3=12。
刚才三个算式,4÷1/2=4×2,4÷1/4=4×4,4÷1/3=4×3,都是整数除以几分之一。仔细观察,从左到右算式发生了什么变化?运算符号变了没有?几分之一和几之间又有什么关系?
(初步归纳方法:整数除以几分之一等于整数乘几分之一的倒数)
2.完善模型
师:我们已经发现,整数除以几分之一可以这样算,如果除以几分之几也可以这样算吗?我们继续研究。
出示例3图,学生列式:4÷2/3。
4÷2/3可以怎样计算呢?请同学们独立在导学单第二题中分一分,画一画,并计算。
(展示学生的画图,说一说想法)
师:每米平均分成3小格,一小格表示1/3米,取两份就是2/3米,我们将4米继续平均分,可以看出,一共可以取6个2/3米,所以4米里面有6个2/3米。
通过画图我们可以知道4÷2/3的答案是6,通过计算我们可以知道4×3/2的答案也是6,所以可以用等号连接。
问:谁能说一说,这里的3/2是什么意思?
(1米可以平均分成3/2段)
3.形成算法
通过研究我们可以看出,除数不管几分之一还是几分之几,其实都是分数。刚才我们一起探索了整数除以分数的方法,现在谁能说一说整数除以分数可以怎样计算?
(板书归纳:整数除以分数等于整数乘分数的倒数)
如果用a÷c/b来表示整数除以分数,谁能说一说,结果等于什么?
(等于a×b/c)
四、深入思考,完善认知(略)
1.巩固性练习
2.应用性练习
3.拓展性练习
五、课堂总结(略)


教学点评
施健老师执教的本节课属于单元整体教学视域下的第二种典型课——方法生长课。与知识种子课相比,方法生长课的关键在于“迁移”,要在上一节课的知识种子基础上进一步“生长”出相应的知识和方法。本课在教学上体现了四个要点:
1.生长性迁移
上一课时,学生学习了分数除以整数,对接整数除法的含义(等分除)帮助学生理解了分数除以整数等于乘整数的倒数。课始,首先复习两道分数除以整数的计算,并回忆计算方法,为接下来继续迁移做准备。
本课例题2的教学以此为基础进一步进行对接与生长。首先继续对接整数除法含义(包含除),提出“4个橙子,每人吃2个,可以分给几人?”“4个橙子,每人吃1个,可以分给几人?”,学生根据整数除法含义列出除法算式后,教师进一步提出“4个橙子,每人吃1/2个,可以分给几人?”进而引出整数除以分数的除法算式。这样,从整数除法到分数除法,从分数除以整数到整数除以分数,新知是在旧知经验的基础上内在生长出来的,方法的迁移也就有了充分的基础。
2.直观性理解
与分数除以整数相比,整数除以分数的算理理解是有一定难度的。施老师充分借助直观教具与直观图形帮助学生理解算理,形成算法。
例题2的教学,借助直观的橙子图片,组织学生动手操作。首先把4个橙子,每2个分一份,分成了2份(4÷2=2);再把4个橙子,每1个分一份,分成了4份(4÷1=4);然后把4个橙子,每1/2个分成一份,分成了8份(4÷1/2=8)。
例题3的教学,继续借助长条图,让学生在学习单上动手画图理解4÷1/3和4÷2/3,学生通过画图和比较,直观理解了除以一个分数可以转化为乘分数的倒数。
3.抽象性概括
抽象性是数学学科的第一特性,因此我们要结合数学学习的过程不断培养学生的抽象概括能力。在学生通过教具演示和动笔画图的直观性理解之后,学生能初步把整数除以分数转化为乘这个分数的倒数,但是总不能每次计算整数除以分数都用直观方式进行,因此需要引领学生逐步抽象概括,形成一般性算法。
由于有了第一课时(分数除以整数)的学习基础,学生已经初步感受到转化的力量,即把分数除以整数转化为乘整数的倒数。因此在本课例题2教学时,结合整数除以几分之一的分数,能比较直观地理解转化为乘几分之一的倒数;而在例题3教学时,让每个学生继续画图理解算理,进而在前面两次转化的基础上把整数除以几分之几的分数转化为整数乘这个分数的倒数。这样的抽象概括,既有前序知识的迁移基础,又有直观模型的对应验证,有利于学生完成从算理到算法的过渡。
4.发展性提升
新课标十分强调数的运算教学重点是理解算理、掌握算法,并特别指出要让学生经历算理和算法的探索过程,同时注重感悟数的运算本质上的一致性。
本课在学生初步理解算理和概括算法后,施老师设计了三个层次的练习,帮助学生形成技能,发展能力,提升思维。巩固性练习主要在于对新知算理和算法的再次“反刍”,通过直观算理和抽象算法的对照,帮助学生进一步形成整数除以分数的运算技能。应用性练习则主要在于把整数除以分数的知识应用到解决实际问题中,在问题解决中培养学生发现和提出问题、分析和解决问题的能力。拓展性练习则由分数除以整数、整数除以分数,进一步让学生猜想分数除法的第三种类型——分数除以分数,并让学生带着问题进行初探,为下一课具体探索分数除以分数的算理和算法作了孕伏和铺垫。
,