作为一名“被迫”爱好科研的临床医生,写论文是完成临床工作后的第二大事。但这时,大多数人都会遇到一个难题,那就是:从实验设计到收集数据和分析数据,都必须用到统计学方法。但是,学校教的那些蜻蜓点水的统计学早就还给了亲爱的老师,要重新拿起书本自学,似乎也不太现实。。。
最好呢,就是有那种略去高深莫测的统计学原理和计算公式(有软件谁要这玩意),用具体鲜活的例子来帮助理解概念,并且直奔解决实际问题的方法。
当面对这么多的数据,该如何开展数据统计分析?选择什么样的方法?我们需要将变量资料与分析方法关联、对应起来。流程如下:

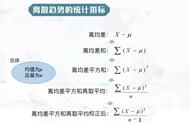
先简单的明确两个基本概念:均数和标准差。举个实际例子:平均收缩压138±7 mm Hg。这里的“138”就是均数;“7”就是标准差。均数代表一组数据的平均值;标准差代表一组数据的离散程度;换句话说,标准差越大,一组数据越参差不齐。统计学上对一组数据都以“均数±标准差”表示。
均数±标准差的计算有一个极其复杂繁琐的公式。我们也并不需要去记住这个公式。现在市面上五花八门的统计学软件,都带有计算“均数±标准差”的功能。我们只需要输入一串原始数据,软件就会自动计算出均数和标准差。我们只需要记住:标准差越小,代表这组数据越整齐;标准差越大,代表这组数据越参差不齐。
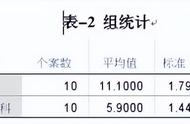
下面来谈谈一种最常用的统计学分析方法:t检验。先看一个实际例子,在临床试验中有A、B两组。33位患者被随机分配到A组(18位)和B组(15位)。研究结果发现,A组数据的均数±标准差为17.4 ± 5.23;B组数据的均数±标准差为25.3 ± 7.35(p=0.03)。
t检验就是检验数据之间究竟有没有显著性差异。而这种差异是通过数学公式推算出来的。但是,这种推算的准确性如何呢?准确性就用P值表示。我们经常看到P﹤0.05或者P﹤0.01什么的。它们究竟表示什么意思呢?P﹤0.05就是表示这种推断的准确性﹥95%;P﹤0.01就是表示这种推断的准确性﹥99%。一般采用0.05作为临界值。P﹤0.05即认为两组数据之间有显著性差异;P>0.05则认为两组数据之间没有显著性差异。所以,t检验的终极目的就是计算P值。
那么,如何计算P值呢?让我们回到上面那个例子,在上面那个例子中,我们一共有6个数据:A、B两组的病例数,均数,标准差。根据这6个数据,就可以计算出P值。现在市面上的统计学软件都可以自动计算出P值。我们要做的只是输入这6个数据,剩下的就交给计算机来做好了。
SPSS中t检验的做法
正态分析

单组样本t检验

配对样本t检验