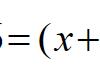趴在学渣的认识高度讲数学,让我们陪着自家的学渣孩子一起逆袭!
我是学渣的学渣老师,简称渣老师。趴在学渣的认识高度讲数学,让我们陪着自家的学渣孩子一起逆袭!
话不多说,今天讲因式分解的十字相乘法。
首先,什么是因式分解。
学渣真有不懂什么是因式分解的,初中课程,时间长了就忘记了。
因式分解就是把加减的式子变成乘积的式子,这个操作过程就是因式分解。
比如这样:X²-Y²=(X Y)*(X-Y)
这个操作过程就是因式分解。
第二,为什么要因式分解。主要是用来解方程,求值。
比如这样:X² 5X 6=0
因式分解:(X 3)*(X 2)=0
所以:X1=-3 X2=-2
看看,本来是一个三项相加的式子,你算不出来X等于多少,通过因式分解这种操作你就能得到X的值。
第三,怎么因式分解
因式分解的方法主要有四种,口诀如下:
首先提取公式,看看能否套公式
十字相乘试一试,分组分得要合适
四种方法反复试,最后必是连乘式
至于配方法什么的,那就是套公式的变形,留着下次再讲。
也就是说,看到因式分解的题,要按照口诀的顺序来思考---
1、提取公式,看有没有可以提取归纳的;
2、套公式,看像能套上哪个公式的(初中高中六年,因式分解方面能用到的基本公式就三个,谢天谢地);
3、就是今天要说的十字相乘法。
4、原题看起来比较乱,但是能分组,分组后再重复以上过程。
5、最后是不是变成了连乘的结果——否则,就是没有完全进行因式分解。
十字相乘法是因式分解中用到的第三种方法,但实际做题中占到的比例很大!为啥?因为能用这种方法分解的问题,都能快速得到答案。
现在重点来了。记口诀:
十字相乘,双手投降
左手拆高,右手拆常
交叉相乘,等于中央
横着一抄,变成连乘
举手投降,是把解题过程形象化,想象左手臂上下分别有两个数字,这两个数字相乘就分别是题目中高次项和常数项。
比如:6X² 11X 3
左手拆高—就是把6X2拆成3X和2X相乘(竖的,相当于左臂上下)
右手拆常—就是把3拆成3和1相乘(竖的,相当于右臂上下)
交叉相乘等于中央,就是把左右拆分的项相乘后相加,看是不是等于中间的项11X
3X 1
2X 3
2X 9X = 11X(相加等于中央)
横着一抄,变成连乘:把上面的结果横向抄写相加
变成连乘式(3X 1)(2X 3),操作完毕。
注意到很多老师或者是教辅资料把十字相乘法进一步分解成了二次项(或者是高次项)带系数和不带系数的,徒增烦恼,大可不必!只要在分解的过程中把X这个未知数带上一起分解就ok(比如3X³,分解成3X和X²)。
最后,在给我们的学渣宝贝讲课时,一定要经常性地用到终极大法---是什么、为什么、怎么办!据我观察,大部分数学不好的孩子形象思维都相对较好,让他们用学语文、学政治的方法理解数学知识很有必要,包括用双手举起的方法来理解十字相乘法。
好了,我是渣老师,关注我,让我们陪学渣一起逆袭!
,