定义1.1 点:点不可以再分割成部分。
定义1.2 线:线是无宽度的长度。
定义1.3 线的两端是点。
定义1.4 直线:直线是点沿着一定方向及其相反方向平铺。
定义1.5 面:面只有长度和宽度。
定义1.6 一个面的边是线。
定义1.7 平面:平面时直线自身的均匀分布。
定义1.8 平面角:平面角是两条线在一个平面内相交所形成的倾斜度。
定义1.9 直线角:含有角得到两条线成一条直线时,其角称为直线角(平角)。
定义1.10 直角与垂线:一条直线与另一条直线相交所形成的两阾角相等,两角皆称为直角,其中一条称为另一条的垂线。
定义1.11 钝角:大于直角的角。
定义1.12 锐角:小于直角的角。
定义1.13 边界:边界是物体的边缘。
定义1.14 图形:由一个边界或几个边界围成的。
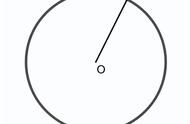
定义1.15 圆:由一条线包围着的平面图形,其内有一点与这条线上任何一个点所连成的线段都相等。
定义1.16 这个点叫圆心。
定义1.17 直径是穿过圆心、端点在圆上的任意线段,该线段将圆分成两等分。
定义1.18 半圆:是直径与被它切割的圆弧围成的图形。半圆的圆心与原圆心相同。
定义1.19 直线图形是由线段首尾顺次相接围城的。三角形是由三条线段围成的,四边形是由四条线段围成的,多边形是由四条以上的线段围成的。
定义1.20 三角形中,三条边相等的称等边三角形,两条边相等的称等腰三角形,各边都不相等的称不等边三角形。
定义1.21 三角形中,有一个角为直角的是直角三角形;有一个角为钝角的称钝角三角形;三个角都为锐角的为锐角三角形。
定义1.22 四边形中,四个边相等并四个角为直角的称为正方形;四角为直角,但边不完全相等的为长方形(也叫矩形);四边相等,角不是直角的未菱形;两组对边、两组对角相等的为平行四边形;一组对边平行,另一组对边不平行的称为梯形。
定义1.23 平行直线:在同一个平面内向两端无限延长不能相交的直线。
公设1.1 过两点可以作一条直线。
1.2 直线可以向两端无限延伸。
1.3 以定点为圆心及定长的线段为半径可以作圆。
1.4 凡直角都相等。
1.5 同平面内一条直线和另外两条直线相交,若在直线同侧的两个内角之和小于180°,则这两
条直线经无限延长后在这一侧一定相交。
公理1.1 等于同量的量彼此相等。
1.2 等量加等量,其和仍相等。
1.3 等量减等量,其差仍相等。
1.4 彼此能够重合的物体是全等的。
1.5 整体大于部分。
关于定义《几何原本》始于一系列定义,这些定义分为三类,第一类指明某些概念,比如指派术语点、线、面的。第二类是原概念衍生的新概念。第三类是性质说明型定义,如定义1.4。
关于公设公设是自明的,意即无需证明的显在事实,尤其表现在平面几何中。公设内容多为作图。

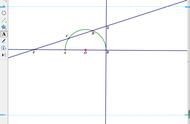
说到作图,《几何原本》不同于后来的数学著作,它的推理过程不仅仅是思维活动,其中还有试验型手动操作。公设1.1直尺过两点作直线对应思维中的两点确定一直线;公设1.3圆规以定点为圆心、以定长线段为半径可以作圆对应于思维中的已知圆心和半径可以确定一个圆。《几何原本》限定尺规作图是因为一切推理的依据是定义、公设和公理,尺规作图实际上是公设1.1和1.3的实操。那么,问题来了。为什么我在做1 1 2=4的推理时只需要脑中的思维活动就可得到正确结果而不需要用石子去摆弄,《几何原本》却需要逻辑推理加手动实操才能得到正确结果?这是因为所谓演绎推理是依据基本规则在思维中对事物的性质进行推演,可以理解为思维的试验,这是一系列环环相扣的逻辑链。由于依据整数的运算法则,对数字进行思维试验就可以获得结果,所以没必要实操。而《几何原本》中的推理逻辑链条并不完整,有些中间结果需要采用实操结果而不能靠逻辑推理得到,这有点类似于逻辑推理中还夹杂着试验结论。典型的是在已知线段做等边三角形中,并没有论证两个圆是否存在交点,直接以作图结果显示有交点作为下一步推理的依据。这表明《几何原本》的推理并不是严密的演绎推理系统,在一些环节还没有摆脱经验性。但放在它诞生的时代和考虑到它的开天辟地的意义,它可以作为演绎推理系统的标杆。
关于量与公理
公理也是自明的,涉及各种不同类型的大小。线段的量出现得最频繁,另一些量是直线的角和面。
关于抽象层级
如果把演绎推理系统比作一棵大树,最基础的定义、公设、公理就是这棵大树的根,它们是最底层的,这里面所说的点和线是高度抽象意义和普遍性上的概念,不是某个特定情形中的点和线。定义、公设、公理具有最高的抽象层级和普遍性。所谓的命题描述了各种特定的情形,这些情形根据抽象层级的不同分别构成了大树的树干、树枝和树叶。演绎推理是从抽象层级高的判断得到更加具体的抽象层级低的判断。公理化的演绎推理系统是一个包含了各种与底层抽象原则相容的具体组合情形的树形结构,是各种可能模式的树形集合,所以具有普遍性和先验性。这也是数学为什么能够作为工具大量应用于科学研究的原因,是为什么数学的同一模式可以出现在不同领域的原因,是数学为什么可以预测还没有被观察到的结果的原因!
尺规作图欣赏