一道初中几何题-与圆相关的线段关系
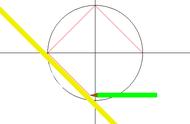
已知一个圆O,其圆心为O, CB经过点O, B在圆上, 且AB垂直于CB, ADOE是一条直线, P是AB上的一点, 且AP=AD, AB的长度是圆的半径的两倍, 证明:


证: 设圆的半径为r, 那么AB=2r,
根据AB垂直于CB, B在圆上,且CB是直径, 那么AB是圆的切线。利用切线定理:

设AP=x, 那么带入上面的等式,

整理一下这个等式为:

而AB=2r,
PB=AB-AP=2r-x,
所以证得,

一道初中几何题-与圆相关的线段关系
已知一个圆O,其圆心为O, CB经过点O, B在圆上, 且AB垂直于CB, ADOE是一条直线, P是AB上的一点, 且AP=AD, AB的长度是圆的半径的两倍, 证明:


证: 设圆的半径为r, 那么AB=2r,
根据AB垂直于CB, B在圆上,且CB是直径, 那么AB是圆的切线。利用切线定理:

设AP=x, 那么带入上面的等式,

整理一下这个等式为:

而AB=2r,
PB=AB-AP=2r-x,
所以证得,














Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.