第一单元:负数
1、正数:如3、500、2,5.33,45,0.6等这样大于0的数叫做正数,前面可以加上“ ”,也可以省略。
2、负数:如-3、-500、-2,-5.33,-45,-0.6等这样的数叫做负数。负数小于0。
3、负数与正数表示意义相反的量,任何正数前添上负号“-”都会变成负数。
4、在直线上,负数都在0的左侧,所有的负数都比0小,正数都在0的右侧,所有的正数都比0大。负数<0<正数。

5、0既不是正数,也不是负数。
6、正数和负数的读法:
5 读作:正五
-5 读作:负五
第二单元:百分数(二)
1、折扣:商品按原定价格的百分之几出售,叫做折扣。通称“打折”。
几折就表示十分之几,也就是百分之几十。
几几折就表示十分之几点几,也就是百分之几十几。
例如:八折==80﹪ 六折五=0.65=65﹪
2、成数:农业收成,经常用“成数”来表示。现广泛应用于表示各行各业的发展变化情况。
几成就表示十分之几,也就是百分之几十。
几成几就表示十分之几点几,也就是百分之几十几。
例如: 二成=20% 三成五=35%
3、税率
(1)应纳税额:缴纳的税款叫做应纳税额。
(2)税率:应纳税额与各种收入中应纳税部分金额的比率叫做税率。
(3)应纳税额的计算方法:应纳税额 = 应纳税部分金额 × 税率
4、利率
(1)本金:存入银行的钱叫做本金。
(2)利息:取款时银行多支付的钱叫做利息。
(3)利率:单位时间内的利息与本金的比值叫做利率。
(4)利息的计算公式:利息=本金×利率×存期
(5)本息和=本金 利息=本金×(1 利率×存期)
第三单元 圆柱和圆锥
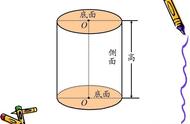
1、圆柱:以矩形的一边为轴,旋转一周所围成的立体图形,叫圆柱。如蜡烛、石柱、易拉罐等。

圆柱由3个面围成。圆柱的上、下两个面叫做底面;圆柱周围的面(上下底面除外),叫做侧面;圆柱的两个底面之间的距离叫做高。
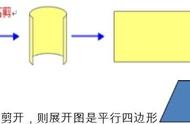
2、圆柱的侧面展开图:

3、圆柱的侧面积:
圆柱的侧面积=底面的周长×高,S侧=Ch(注:c=πd=2πr)
4、圆柱的表面积:
圆柱的表面积=圆柱的侧面积+两个底面的面积
S表=S侧+2S底=2πr(h+r)
5、圆柱的体积:圆柱所占空间的大小,叫做这个圆柱体的体积。
圆柱的体积=底面积×高
V=Sh或V=πr²h;
6、圆锥:以直角三角形边为轴,旋转一周所围成的立体图形,叫圆锥。生活中经常出现的圆锥有:沙堆、漏斗、帽子等。

7、圆柱与圆锥的关系:与圆柱等底等高的圆锥体积是圆柱体积的三分之一。体积和高相等的圆锥与圆柱(等低等高)之间,圆锥的底面积是圆柱的三倍。体积和底面积相等的圆锥与圆柱(等低等高)之间,圆锥的高是圆柱的三倍。底面积和高不相等的圆柱圆锥不相等。
第四单元:比例
1、像2.4:1.6=60:40这样表示两个比相等的式子叫做比例。
2、组成比例的四个数,叫做比例的项。两端的两项叫做外项,中间的两项叫做内项。
3、比例的基本性质:在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
4、解比例:根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个数比例中的另外一个未知项。求比例中的未知项,叫做解比例。
5、比例尺:图上距离与实际距离的比叫做比例尺。
图上距离:实际距离=比例尺
图上距离÷比例尺=实际距离
实际距离×比例尺=图上距离
6、比例尺按书写形式分为数值比例尺和线段比例尺;按功能分为放大比例尺和缩小比例尺。
7、放大或缩小后的图形与原图比较:形状相同,大小不同。
8、画一个图形放大与缩小后的图的步骤:
①按比例计算放大或缩小后的图形相应边的长度;
②按相应边的长度画出放大或缩小后的图形。
(有时还需要测量有关对应角的度数。注意:放大或缩小后的图形与原图形状不变,就是对应角的度数不变。)
9、成正比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,他们的关系叫做正比例关系。y/x=k(一定)
10、成反比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,他们的关系叫做反比例关系。用字母表示xy=k(一定)
第五单元:数学广角——鸽巢问题
1、鸽巣原理是一个重要而又基本的组合原理, 在解决数学问题时有非常重要的作用。

利用公式进行解题
①物体个数÷鸽巣个数=商……余数 至少个数=商 1
②物体个数÷鸽巣个数=商 至少个数=商
2、摸2个同色球计算方法:
①极端思想: 用最不利的摸法先摸出两个不同颜色的球,再无论摸出一个什么颜色的球,
都能保证一定有两个球是同色的。
②公式:
两种颜色:2+1=3(个)
三种颜色:3+1=4(个)
四种颜色:4+1=5(个)
3、摸n个同色球计算方法
要保证摸出n个同色的球,最坏情况,每个颜色的球都摸出了(n-1)个,再摸一个就能保证。
摸球数=颜色数×(n-1)+1
,