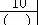数学是思维的体操,解决数学问题是一种智慧的游戏。通过数学解题的启发,打开思维,培养思维敏捷性,提高解题水平,达到培养数学思维和逻辑推理能力,是学习数学的目的所在,也是数学的魅力所在。
例1:计算24×25×26
解:原式=(25-1)×25×(25 1)
=(25²-1)×25
=25²×25-25
=625×25-25 (625个25减去一个25,等于624个25)
=624×25
=156×(4×25)
=156×100
=15600

例5:已知x³ x²=392,则x³=?
这看似是一道初中的一元三次方程题(印度初中数学竞赛题),超出小学生解题范围。但用小学数学的乘法分配律及分解质因数的方法,也可以非常简单地解答出来。
解:x³ x²=392
x²(x 1)=392
因为392=2×2×2×7×7
=7²×(7 1)
所以x=7
x³=7³=343
例6:如果a、b均为质数,且3a 7b=41,则a b的值是多少?
解法一:先进行奇偶性分析。
3a 7b=41,41是奇数,只有奇数 偶数=奇数,说明3a的积与7b的积中有一个是偶数,亦即a或b中有一个是偶数。
即是质数又是偶数的数,只有2。那么a=2或b=2。
假设a=2,7b=41-6=35,b=5,符合题意。
所以a b=2 5=7。
再假设b=2,3a=41-14=27,a=9,9不是质数,不符合题意。
所以本题答案:a b的值是7。
解法二:因为3a 7b=41,那么a=(41-7b)÷3,可知b为小于6的质数。
小于6的质数只有5和2。
当b=2时,a=9(不符合题意)。
当b=5时,a=2,a b=2 5=7。
例7:a、b、c、d为整数,且ac bd ad bc=1997,求a b c d=?
解:ac bd ad bc=1997
ac bc bd ad=1997
c(a b) d(b a)=1997
(a b)(c d)=1997
1997=1×1997=1997×1 (1997为质数)
所以a b=1,c d=1997;或a b=1991,c d=1。
所以a b c d=1 1997=1998或a b c d=1997 1=1998
有人说数学很难。但只要多见题型,找对解题方法,数学也很简单。
数学其实挺好玩!
,