圆柱训练题
班级: 姓名:
一、填空
1. 1、800 毫升=( )升 5.4 平方分米=( )平方厘米
2.8 立方米=( )立方分米 5 平方米 4 平方分米=( )平方米
2. 把圆柱切开、再拼起来,能得到一个( )。长方体的底面积等于圆柱的( ),
长方体的高等于圆柱的( ),因为长方体的体积=底面积×高,所以圆柱的体积=
( ),用字母表示是( )。
3.把圆柱体的侧面展开,得到一个( )。圆柱的侧面积等于( )乘高。
4.圆柱的底面半径扩大到原来的 2倍,高不变,它的侧面积扩大到原来的( )倍。
5.已知圆柱的底面直径是 6 厘米,高是 5 厘米,侧面展开图的长是( )厘米,宽是( )
厘米。
6. 一个圆柱体,底面半径是 4厘米,高是 10 厘米,它的侧面积是( )平方厘米。
7. 一个圆柱体的底面半径是 10 厘米,高是 20 厘米。它的的表面积是( )平方厘米,
8. .把一张长 5分米,宽 4 分米的长方形纸,卷成一个圆柱形纸筒,这个纸筒的侧面积是( )
平方分米。
9. 把一张长 5 分米,宽 4 分米的长方形纸,以它的宽所在的直线为轴旋转一周,得到一个圆柱
体,这个圆柱体的表面积是( )平方分米,体积是( )立方分米。
10.一个圆柱的底面周长是 31.4 分米,高是 10 分米,它的底面积是( )平方分米,
侧面积是( )平方分米,体积是( )立方分米。
11. 一个圆柱的体积是 113.04 分米,底面积是 6.28 平方分米,它的高是( )平方分米。
12.两个底面积相等的圆柱,一个高为 5.6 分米,体积为 84 立方分米。另一个高为 6 分米,它
的体积是( )立方分米。
13.一个圆柱体,它的高增加 3 厘米,侧面积就增加 18.84 平方厘米,这个圆柱体的底面半径是
( )厘米,底面积是( )平方厘米.
14.一个高 5 厘米的圆柱体,沿底面直径将圆柱体锯成两块半圆柱,其表面积增加 40 平方厘米,
原来这个圆柱体的体积是( )立方厘米。
二、判断
1. 一个圆柱的高缩小到原来的1
2,底面半径扩大2倍,它的表面积、体积不变( )
2. 圆柱体的侧面积等于底面积乘以高。 ( )
3. 把一个圆柱切成两半,表面积和体积都增加了。 ( )
4、圆柱体的体积公式是由长方体的体积计算公式推导而来的。 ( )
5、长方体、正方体、圆柱体的体积都可以用底面积乘高的方法来计算。 ( )
三、选择正确答案的序号填空。
1、圆柱体的底面半径扩大 2倍,高不变,它的体积扩大( )倍.
A.2 B. 4 C. 6 D. 8
2、甲乙两人分别利用一张长 20 厘米,宽 15 厘米的纸用两种不同的方法围成一个
圆柱体(接头处不重叠),那么围成的圆柱( )
A.高一定相等 B.侧面积一定相等 C.侧面积和高都相等 D.侧面积和高都不相
3、等底等高的圆柱体、正方体、长方体的体积相比较,( ).
A、正方体体积大 B、长方体体积大 C、圆柱体体积大 D、一样大
4、圆柱体的底面半径和高都扩大 2 倍,它的体积扩大( )倍.
A.2 B. 4 C. 6 D. 8
5、把一个棱长是 2 分米的正方体削成一个最大的圆柱体,它的侧面积是( )
平方分米。
A.6.28 B.12.56 C.18.84 D. 25.12
四、解决问题
1、一个圆柱的侧面积是 12.56 平方米,底面半径是 4 分米,它的高是多少分米?
2、 一个圆柱形的沼气池,底面直径 4 米,深 3 米。在池的四壁与下底面抹上水泥。
(1)抹水泥部分的面积是多少平方米?
(2)修建这样的沼气池要挖土多少立方米?
3 一个圆柱粮囤,从里面量得底面半径是 2 米,高是 3 米。如果每立方米玉米约重 750 千克,
这个粮囤能装多少吨玉米?
4、把一种空心混凝土管道,内直径是 4 分米,外直径是 8 分米,长 3 米,求浇制
100 节这种管道需要多少方混凝土?
5、做一个无盖的圆柱形铁皮水桶,高 30 厘米,底面直径 40 厘米,做这个水桶至
少要用多少平方分米的铁皮?这个水桶能装多少千克的水?(1 立方分米水重 1 千
克)
6、一个高是 20 厘米圆柱体,如果把它的高截短 3 厘米,它的表面积减少 94.2 平
方厘米。原来圆柱的体积是多少立方厘米?
7、一个圆柱形水槽,底面半径是 8 厘米,水槽中完全浸没着一块铁件,当铁件取
出时,水面下降了 5 厘米。这块铁件的体积是多少立方厘米?
圆柱表面积、体积提高训练
班级: 姓名:
一、复习
1、一个圆柱体,把它的高截短3cm,它的表面积减少94.2平方厘米。这个圆柱体的底面积是多少
平方厘米?
2、一个圆柱体的高是 30 厘米,底面半径是 4厘米,如果沿着直径劈成两个半圆柱体,它的表面积将增加多少平方分米?
3、一个圆柱底面半径为 5 厘米,把它的高增加 3 厘米后侧面积增加多少平方厘米?
圆柱的侧面积:S侧=Ch=πdh=2πrh
圆柱的表面积:S表=2πr²+2πrh =2πr(r+h)
例 1、一个圆柱体的体积是50.24立方厘米,底面半径是 2 厘米.将它的底面平均
分成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平
方厘米? ( π 3.14 )
4、一个圆柱体的体积是 141.3 立方厘米,底面半径是 3 厘米.将它的底面平均分
成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方
厘米?
5、将一个底面半径是 3 分米的圆柱体的底面平均分成若干个扇形后,再截开拼成
一个和它等底等高的长方体后,表面积增加了 18 平方分米,这个圆柱体的体积是
多少立方分米?
例 2、一段圆柱体木料,如果截成两个小圆柱体,它的表面积增加 6.28 平方厘米,如果沿着直径劈成两个半圆柱体,它的表面积将增加 80 平方厘米,求原圆柱体的表面积?
6、一个圆柱体,如果沿着直径劈成两个半圆柱体,它的表面积将增加 200 平方厘米,如果截成
两个小圆柱体,它的表面积增加 25.2 平方厘米,求原圆柱体的表面积?
7、一个圆柱体,如果截成两个小圆柱体,它的表面积增加了 12.56 平方厘米,如果沿着直径劈
成两个半圆柱体,它的表面积将增加 100 平方厘米,求圆柱体的表面积?
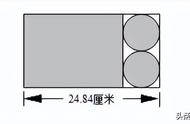
例 3、下面是一张长方形纸板,按图示剪下阴影部分刚好能做成一个圆柱体,求做
好的圆柱体的表面积。
8、有一张长方形铁皮,剪下两个圆及一个长方形,正好可以做成一个圆柱,这个
圆柱的底面半径为 10 厘米,那么原来长方形铁皮的面积是多少平方厘米?
,