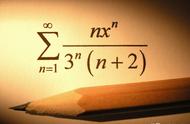这个结果是通过一些复杂的数学技巧和方法得出的,包括复数解析、正规化和解析延拓等。这个结果可以在数学和物理学中找到应用,尤其在量子场论和弦论等领域。
这个结果并不意味着我们可以将级数 1 2 3 4 ... 的每一项直接相加得到 -1/12。这个结果是通过对黎曼ζ函数的解析延拓和正规化技术的运用得到的。在实际应用中,我们必须小心使用这个结果,确保理解背后的数学概念和技术,并将其适当地应用于具体问题。

黎曼ζ函数(Riemann zeta function)是一个特殊的数学函数,最早由德国数学家伯尔纳德·黎曼(Bernhard Riemann)在19世纪提出和研究。黎曼ζ函数在复平面上定义,并在数论、复分析和物理学等领域中具有广泛的应用。
黎曼ζ函数的定义如下:
ζ(s) = 1^(-s) 2^(-s) 3^(-s) 4^(-s) ...
其中,s 是一个复数,实部大于 1。这个函数是由无穷级数的和所定义的,其中每一项是自然数的倒数的幂。
然而,黎曼ζ函数的特殊之处在于它可以通过解析延拓(analytic continuation)的方法,将其定义扩展到复平面上的其他区域。在解析延拓中,我们可以使用复数解析的技术将一个函数在定义域内的性质推广到更大范围。
黎曼ζ函数在实部大于 1 的区域上有简单的解析表示,但当实部小于或等于 1 时,黎曼ζ函数的定义不再适用。通过解析延拓,我们可以将黎曼ζ函数的定义拓展到复平面上的其他区域。

黎曼ζ函数在数学中的研究具有深远的影响。特别重要的是黎曼猜想(Riemann Hypothesis),它提出了一个关于黎曼ζ函数零点的猜想。黎曼猜想认为,除了 s=1 外,所有使黎曼ζ函数的值为零的非平凡复数都具有实部为 1/2。黎曼猜想至今仍未得到证明,但它对数论的发展产生了深远的影响,并与素数分布等数论问题有密切关联。
黎曼ζ函数在物理学中也有广泛的应用。例如,在量子场论和弦论中,黎曼ζ函数出现在计算真空能、场论振幅和量子修正等问题中。它在处理发散积分和规范化等数学技术中扮演着重要的角色。
总结起来,黎曼ζ函数是一个由无穷级数定义的特殊函数,通过解析延拓可以将其定义扩展到复平面上的其他区域。它在数学和物理学中具有广泛的应用,涉及到复分析、数论、量子场论和弦论等领域。

ζ(-1) = -1/12 这个结果在物理学中有特定的意义,尤其在量子场论和弦论等领域中的物理计算中具有重要的应用。
真空能和量子场论:在量子场论中,真空能是指真空态中的能量。真空能的计算经常涉及发散的积分和级数求和,这些发散需要通过正规化技术进行处理。黎曼ζ函数在正规化真空能计算中起到重要的作用,特别是在减法正规化(subtraction regularization)中,其中ζ(-1) = -1/12 被用作一个重要的数值。