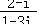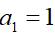数学分析研究的基础是极限。
事实上,牛顿已经给出了极限的想法,但如前面引用的那样,牛顿是用极限解释无穷小量。对于牛顿和莱布尼茨特别关注的无穷小量,法国数学家达兰贝尔的态度是十分明确的,在《百科全书》的“微分”条目中,他认为“关于无穷小量所作的假设只是为了推理的简化”,“那些量(导数)不代表无穷小量之商,而是两个有限量之比的极限”。1786年,惠利尔用符号表达了这个定义,即瞬时速度=dy/dx=lim(△t→0)[(f(t0 △t)-f(t0))/△t]。接下来,达兰贝尔又在“极限”条目中明确指出:
当一个量以小于任何给定的量逼近另一个量时,可以说后者是前者的极限,......极限理论是微分学真正形而上学的基础......
柯西在他1821年出版的《分析教程》中则给出了我们今天仍然在使用的定义:
一个变量逐次所取得值无限趋向于一个固定值,使得所取的值与该定值要多小就多小,那么,就称这个定值为所有其他值的极限。
然后,柯西以及魏尔斯特拉斯用数学符号清晰地表达了上面的意思。假定一个变量的取值依次为:
1/1,1/2,1/3,1/4,......
这就形成了一个数列,我们用{1/n}表示这个数列,其中n由小到大依次取正整数。虽然这个数列中的每一项都大于0,但随着n的增大这个数列的取值可以无限地解决0,于是就定义这个数列的极限为0。我们可以把这些话语进一步用符号来阐述:
对于任意ε>0,不管ε是多么的小,只要不是0,就存在N(比如令N为大于1/ε的正整数),这样当n>N时,就有
|(1/n)-0|<ε
表示为lim(n→∞)1/n=0
这表明1/n与0之间的差可以任意的小,于是称0为数列{1/n}的极限。这种想法显然可以推广到一般,下面给出一个数列收敛到某个极限的定义:
对于数列{an}和数值a,如果对于任意ε>0,均存在N,使得当n>N时,有
|an-a|<ε
则称数列{an}是收敛的,并称a为数列{an}的极限,表示为
lim(n→∞)an=a
定义中所说的“对于任意ε>0”实质是在说“对于无论怎样小的正数ε”,这一点与牛顿最初的想法是一致的,只是避免了使用“无穷小量”这样很难给出定义的词语。因此,数列收敛的定义阐述的是这样一个事实:任意做一个包括数值a的区间,无论这个区间怎样小,都能找到一个N,使得数列中aN以后的所有项都在这个区间之内,则称a为这个数列的极限。
下面我们来分析一个数列{an}收敛的条件,由定义容易得到:当n趋向无穷时,数列中相领两个项的差an 1-an将趋向于0,这是因为由三角不等式可以得到
|an 1-an|≦|an 1-a| |an-a|<2ε
而ε是一个可以任意的小的量。但是,这只是一个必要条件,即任何收敛数列都必须满足的条件,如果要把这个条件作为收敛准则,还需要证明充分性。事实上,这个条件是不充分的,即满足这个条件的数列不一定收敛,我们将在下面进一步讨论无穷级数时给出一个例子。一个判断数列收敛的,简洁明快的充分必要条件是柯西给出的,被称为柯西准则:
一个数列{an}收敛的充分必要条件是,对于任意给定的正整数k都有:当n→∞时,
an k-an→0
这比刚才说的必要条件的要求更强了,因为在必要条件中只是要求k=1。
这就是第二步的抽象。可以看到,通过定义和符号的表达,已经完全摆脱了对于物理或者几何直观的依赖,有了这些基本表达,就可以摆脱牛顿和莱布尼茨以来数学出现的“解释不清”的尴尬局面了。