我们前面已经证明了自然数的倒数之和是无穷发散的,是不收敛的,但它与In(1 n)之差却是一个常数,即著名的欧拉常数

但是连续偶数的倒数之和是否收敛呢?如下图所示

你会发现这些偶数的倒数之和的2倍等于自然数的倒数之和,既然自然数的倒数之和是发散,那么偶数的倒数之和肯定是发散的,

那么连续奇数的倒数之和是否收敛呢?你会发现1>1/2,1/3>1/4,1/5>1/6.......(1/(n-1))>1/n

因为1/2 1/4 1/6 ....是发散的,所以连续奇数的倒数之和肯定也是发散的
我们前面已经证明了自然数的倒数之和是无穷发散的,是不收敛的,但它与In(1 n)之差却是一个常数,即著名的欧拉常数

但是连续偶数的倒数之和是否收敛呢?如下图所示

你会发现这些偶数的倒数之和的2倍等于自然数的倒数之和,既然自然数的倒数之和是发散,那么偶数的倒数之和肯定是发散的,

那么连续奇数的倒数之和是否收敛呢?你会发现1>1/2,1/3>1/4,1/5>1/6.......(1/(n-1))>1/n

因为1/2 1/4 1/6 ....是发散的,所以连续奇数的倒数之和肯定也是发散的


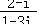










Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.