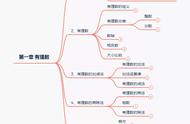
首先声明,这不是标题党。
我们知道,整数包括正整数,0,负整数。
而传统思维里面,自然数就是正整数。
那既然如此,为什么说整数的个数跟自然数个数一样多呢,明显就是2倍再多个0啊。
其实这个在高等数学里面,是正确的。涉及到无限集合和有限集合的区别。
这里面有个非常有意思的思想实验。
希尔伯特的旅馆为了更好地解释无限集合与有限集合的区别,希尔伯特在他1924年1月的一次演讲中,举了一个有趣的具有无穷多个房间的“希尔伯特旅馆”的例子。
希尔伯特假设有个旅馆,里面有无数个房间,就是无数个。
酒店采取的办法是,将原来1号房间的客人移到2号房间,2号房间的客人移到3号房间,3号房间的客人移到4号房间,让他们一直移下去……

你把整数按照这个顺序排序:0,1,-1,2,-2,3,-3......
A、这里就好像是分别叫做0,1,-1,2,-2,3,-3......的客人。
B、然后旅馆的房号,按照1,2,3,4,5,6,7......进行编号。
那么,A里面的客人,按顺序住进B里面的房号,你会发现,是可以一 一 对应的。

用数学函数表示就是:
A>0时,B=2A
A<=0时,B=2|A| 1
因此B跟A,是可以一 一对应的,不管A等于多少,都有个B跟它对应。
也就是说,整数里面,任何一个数,都可以找到一个自然数与之对应。
那么,就是个数是一样多的。
实际上,在无限集合中,我们可以说整数集合与自然数集合里面的元素一样多。
这个跟有限集合里面的“个数”要区别开来理解。
说明了无限集合的性质与有限集合的性质完全不相同。


下一篇我打算写一下高等数学在日常生活中究竟有什么用,实实在在的作用。
如果你对高等数学有点兴趣,请评论留言,我以后用人话写多一些。。
,