提到井字棋,想必大家都不陌生,就是两个玩家轮流在一个井字型的 9 宫格里画 x 和 o,当某一方的棋子连成了一条线(横向,竖向和对角线),那么该方获胜,如果格子被填满也没有人成功连线,则平局。这次我们来学习如何用 micro:bit 实现一个井字棋小游戏。
通过 我们实现了光标移动,A B 玩家轮流下棋的逻辑,通过 我们学习了处理异常情况,比如当前光标位置已经有棋子了,显示一个 X,不让玩家再在当前位置下棋,当棋盘满了没有玩家获胜就显示一个 “Draw Game” 表示平局,这节教程我们将会实现井字棋游戏剩下的部分,判断输赢,这节教程会稍微难一些,涉及到一个简单的算法来算输赢,我会用一些图形来解释原理方便理解,不要被算法两个字吓到,没那么难啦,如果实现的过程中碰到什么问题可以在我的公众号给我留言,让我们开始吧
什么是算法
算法,英文名是 Algorithm,表示的是为了解决特定问题的一组指令的集合,一个算法通常会有五个特征。
- 有限性(Finiteness):一个算法必须保证执行有限步之后结束。
- 确切性(Definiteness): 一个算法的每一步骤必须有确切的定义。
- 输入(Input):一个算法有零个或多个输入,以表示运算对象的初始情况,所谓零个输入是指算法本身给定了初始条件。
- 输出(Output):一个算法有一个或多个输出。没有输出的算法毫无意义。
- 可行性(Effectiveness): 一个算法的任何计算步骤都是可以被分解为基本可执行的操作,每个操作都能够在有限时间内完成。
对于井字棋游戏来说,输入就是当前棋盘上棋子的坐标,输出就是有没有一方胜出或平局。
如何计算井字棋的输赢
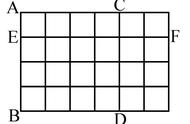
井字棋的输赢判定有很多种不同的算法,这里我选了一种比较好理解的,我叫它计分法。井字棋的赢棋情况一共有 8 种,横竖各 3 条线加 2 个对角线,来看下面的图:

搭配这张坐标图,得到 8 种情况每种对应的 3 个棋子坐标如下


具体算法是
- 初始化一个有 8 个元素的数组,每个元素都是 0
- 在每次落子时,判断落子的 x 坐标和 y 坐标符合上面哪条规律,给对应数组元素编号(数组元素是从0开始的,还记得吗)的数字加 1 或者减 1,这里规定 如果是玩家 A 下的棋,则 加 1,如果是玩家 B 下的棋,则减 1,需要注意的是上面的规则可能会同时满足,比如 (4,4) 同时满足 3、6、7 这 3条规则
- 遍历这个数组,如果有其中一个数字是 3 或者 -3,就表明有玩家胜出了,如果为 3 则玩家 A 胜出,如果是 -3 则为玩家 B 胜出
- 如果下到 9 个格子都满了也没有胜出,那就平局,平局的逻辑 上节教程 已经处理过啦。
之所以叫计分法,是指当有一方玩家落子之后,给对应的胜负情况计 1 分或计 -1 分,最后判断只要有一方先到 3 分或者 -3 分则胜出,是不是没有那么难呀。
举个例子(如果聪明的你已经理解了,那么就可以跳过下面的例子解释,直接看实现部分啦)
1.玩家 A 在棋盘中间走了一步,即 (2,2),符合编号 2、5、7,则给数组元素编号为 1、4、6的元素分别加 1