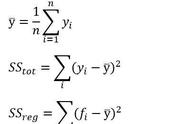最近几期把统计与概率大题中的几大问题做一次总结,大致分为三期内容,分别为线性回归方程问题;二项分布问题;两点分布和正态分布问题。
关于大题中的回归方程,并非都是线性的,在高考或者模拟试题中出现的回归方程大多都是非线性的,而我们只学过线性回归方程中参数和相关系数的求法,因此需要通过换元把非线性转化为线性来处理,这也是此类问题中最常见的一类问题。
无论是新高考还是常规的全国卷,在大题中很少单独考查统计部分,常见的形式是问题分两到三问,前两问涉及统计的知识,最后考查分布列和数学期望,而统计部分除了回归方程还有独立性检验,独立性检验本身没什么难度,就不再单独细说了。
先回顾一下回课本中回归方程相关的基础知识,课本上是从抽样开始讲起,从不同的抽样方式获取样本,计算出样本的数字特征以及图像特征,统计出两个变量之间的对应关系后制作成散点图,根据散点图判断两变量之间的相关关系和相关强度,在从统计得到的数字特征中计算出线性回归方程(非线性转化为线性),最后用线性回归方程来预测数据,若但看线性回归方程这块内容,知识点非常少,就y=bx a中a,b的求法以及相关系数r的求法,在考试中题目的设置也无非围绕这展开。
第一种:考查公式的拆解求值加预测
第二种:考查将非线性转化为线性回归方程后求值加预测
翻遍了五十多套题目,从中选出五道题目分享如下:


第一题这种就是纯粹的计算问题,在考试中一般不会出现这种题目,若出现也是会给出一些已知的数据,根据数据求值,值得一说的是通过用公式来求b,在求a的时候要么直接用a=y-bx来求,要么将样本的均值点代入,像这种简单直接的求值问题在高考中几乎不可能出现了。

若样本可用多个回归方程来拟合,选择变量相关性最强的那个,即相关系数绝对值越接近于1的回归方程。