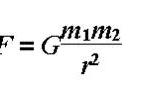假设有两个物体,质量分别为m1和m2,它们之间的距离为r。根据观察,我们可以推测两个物体之间的引力与它们的质量和距离有关。
第一步,我们考虑一个物体对另一个物体施加的引力。根据牛顿第二定律,力等于质量乘以加速度。在这种情况下,加速度是由引力产生的。所以,物体1对物体2施加的引力可以表示为:
F = m2 * a
第二步,我们需要找到加速度a的表达式。根据牛顿第二定律,加速度等于力除以质量。将这个表达式代入第一步的方程中,我们得到:
F = m2 * (F / m1)
现在我们可以简化这个方程。将两边的m2消去,我们得到:
F * m1 = m2 * F
第三步,我们要找到引力F的表达式。根据观察,我们可以假设引力与两个物体质量的乘积成正比,与它们之间的距离的平方成反比。所以,我们可以写成如下形式:
F = G * (m1 * m2) / r^2
其中,G是一个常数,称为万有引力常数。将这个表达式代入第二步的方程中,我们得到:
G * (m1 * m2) / r^2 * m1 = m2 * G * (m1 * m2) / r^2
通过化简,我们可以得到:
G * m1 / r^2 = G * m2 / r^2
这意味着物体1对物体2施加的引力与物体2对物体1施加的引力大小相等,但方向相反。这是牛顿第三定律的结果。
综上所述,根据这个推导过程,我们可以得出万有引力定律的数学表达式:
F = G * (m1 * m2) / r^2
这个方程描述了两个物体之间的引力作用,其中F是引力的大小,m1和m2是两个物体的质量,r是它们之间的距离,G是万有引力常数。
,