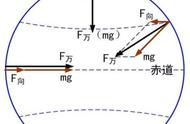
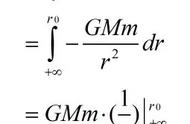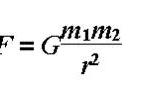牛顿的万有引力定律,他用G作为引力常数,用数学方法定义了万有引力定律。
引力是导致恒星之间扩散物质缓慢坍缩并形成新的氢聚变机器(又名恒星)的粘合剂,它是将星系粘合在一起的粘合剂,也是我们自己的地球每年绕太阳运行的原因。
重力也是艾萨克·牛顿爵士著名的“苹果”故事的关键。
有一天,牛顿在英国林肯郡闲逛时,看到一个苹果从树上掉下来。
在接下来的几年里,他会告诉许多熟人——比如伏尔泰和传记作家威廉·斯图克利——他关于引力本质的伟大著作是受到这个平凡的小事件的启发。牛顿的助手约翰·康杜伊特写道:
他突然想到,同样的引力(使苹果从树上掉到地上)并不局限于离地球一定的距离,而一定会延伸到比通常认为的更远的地方——为什么不像月亮那么高呢,他对自己说,如果是这样,那一定会影响她的运动,也许会使她保持在自己的轨道上。
就这样,牛顿的万有引力定律奠定了基础。其核心是一种被称为引力常数的现象,又名“大G”或简称为“G”。
方程
在我们解决大G之前,我们应该退一步解释一下牛顿的万有引力定律。
引力是有质量的物体相互吸引的机制。
牛顿意识到,一组给定物体之间引力的强度取决于(a)它们的质量和(b)它们之间的距离。这是他的万有引力定律用数学术语描述的动态。
下面是相关方程:
F = (G x m1 x m2) / r2
“F”代表“重力”;“m1”表示第一个物体的质量;“m2”表示第二个物体的质量;r2是物体1和物体2的质心之间距离的平方的简写。
那"G"呢? 这就是重力常数。
“天啊,G !”
对于任何两个质量,无论是保龄球还是行星,它们之间的引力是由它们的质量、距离和数字G决定的。
多亏了亨利·卡文迪什在18世纪90年代进行的实验,我们现在知道引力常数的数值大约是6.67 x 10 -11牛顿(m2/kg2)。
在这种情况下,术语“牛顿”指的是一种测量单位。一牛顿是使质量为2.2磅(1千克)的物体以每秒3.28英尺(1米)的速度加速所需的力。
牛顿与爱因斯坦
现在,这里有一层细微的差别我们应该承认。你看,万有引力定律并不像它的名字所暗示的那么“普遍”。
牛顿早在17世纪就提出了“我们关于引力的经典图景”,这是“整个宇宙中大多数地方(当然是地球上)物理现实的精确近似值”。
然而,这一理论已经被爱因斯坦的广义相对论所取代,广义相对论是对牛顿引力的改进,它假定物质会使时空本身变形。
这就把我们带到了黑洞。
黑洞的质量是太阳的100多万倍,它以牛顿定律无法解释的方式影响引力。广义相对论已经被证明对它们做出了更准确的预测。
你必须开始修正这样一个事实,即牛顿对引力的描述并不完全适用于极强的引力或非常快的运动。在这种情况下,我们需要转向爱因斯坦的引力图……但只要你不是在看那些极端的例子,艾萨克·牛顿在1686年写下的那个他称之为‘万有引力定律’的方程确实是普遍的。”
,