有些学生在小学时数学成绩比较好,进入初中后,成绩会下降。特别是进入八年级,遇到几何证明题时,常常不知道从何处入手。写题时常丢三落四,证明过程书写不规范,推理不严密。学生出现这些问题的原因有哪些?怎样做才能顺利写好证明过程呢?

我认为要解决问题应从以下几方面入手。
一、对学习过的定义、定理等要掌握牢固。
证明题的书写过程,就是利用已学过的定义、定理等,推理得出问题结论的过程。如果学生对学过的内容掌握的不牢固,看到相关联的内容却得不出相应的结论,就无法证明问题。

在上题中,有“角平分线”一词,就要想到角平分线上的点到角两边的距离相等,从而由已知可得DE=DF。由“垂直平分线”一词就要想到线段垂直平分线上的点,到这条线段两端点的距离相等,从而想到连结DB、DC,则DB=DC,再利用Rt△BDE≌Rt△DFC即可证明EB=CF。
二、书写证明过程,应从已知条件入手。
证明过程的书写,必须从题中的已知条件入手,或者是如对顶角相等、三角形的外角等于不相邻的两内角的和等,这些通过观察图形,利用已学过的定理可直接得到的内容入手写。
同一道证明题的书写过程不是唯一的,但无论怎样书写,都要依据一个原则,必须能由上面的因为,得出下面的所以。
比如,在上题中,已知条件有两个,角平分线和线段的垂直平分线,先写哪个都可以,但一般把添加的辅助线写在前面。
书写步骤可以是:
证明:连结DB、DC
∴DB=DC
∵AD平分<BAC,DE丄AB,DF丄AC,垂足分 别为E、F
∴DE=DF
∴Rt△DBE≌Rt△DCF
∴EB=FC
三、读完题中的已知条件,不知道从哪儿入手去解决问题时,可通过把已知条件在图中做标记,寻找解题思路。
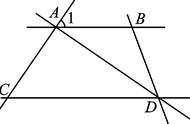
例如:如下图所示,AD是△ABC的高,E为AC上一点,BE交AD于点F,且有BF=AC,FD=CD,求证:BE⊥AC

在上题中,观察所作标记可得Rt△BDF≌Rt△ADC,由两三角形全等可得<FBD=<CAD,再利用<FBD <BFD=<CAD <AFE,<FBD <BFD=90,可得<CAD <AFE=90,从而得<AEF=90,即可证明BE丄AC。