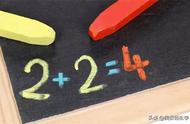1 1/(2×2) 1/(3×3) 1/(4×4) … 1/(n×n) …> 1 [1/(2×2) 1/(3×3)] [1/(4×4) [1/(8×8)] …
我们立即发现,中括号内的项分母是不连续,无法象上面一样进行放缩估计,所以是行不通的!
实际上,我们尝试一下逐项计算:
记S(n)=1 1/(2×2) 1/(3×3) 1/(4×4) … 1/(n×n),
则有
S(1)=1,S(2)= 1 1/(2×2)=5/4=1.25,S(3)= 1 1/(2×2) 1/(3×3) =49/36≈1.36,S(4)=1 1/(2×2) 1/(3×3) 1/(4×4)≈1.42,
S(5)=1 1/(2×2) 1/(3×3) 1/(4×4) 1/(5×5)≈1.46,
什么感觉,好象是越往后增加的越慢,是不是?这说明,这个数列的和可能是有界的!
事实果真如此:
S(n)=1 1/(2×2) 1/(3×3) 1/(4×4) … 1/(n×n)
<1 1/(1×2) 1/(2×3) 1/(3×4) … 1/[(n-1)×n]
=1 (1-1/2) (1/2-1/3) (1/3-1/4) … [1/(n-1)-1/n]
=2-1/n,
显然,无论n如何,2-1/n总小于2,那么可以看出,按这样的分法,小红永远吃到的披萨都不会多于两块!
问题来了,既然这里的S(n)=1 1/(2×2) 1/(3×3) 1/(4×4) … 1/(n×n),单调有界,那么它必有极限,它的极限是多少呢?
事实上,我们可以通过级数或二重积分证明,这个极限值是

猜一猜这个发现是谁最先给出的?
猜到了吗,就是上面提到的那人大名鼎鼎的Euler,真是神一样的Euler!
平方倒数求和最早出现于17世纪意大利数学家蒙哥利(Mengoli P,1626一1686)的《算术求和新法》(1650).
无穷级数

是书中所论形数倒数求和问题中的一个特殊情形。
在发表于19年的论文“具有有限和的无穷级数的算术命题”中,瑞士著名数学家雅各.伯努利(Jacob.Bernoulli,1654一1705)部分重复了蒙哥利的无穷级数工作,在论文最后,伯努利称,尽管级数

的求和问题易如反掌,但奇怪的是,ζ(2)的和却难以求出.他说:”如果有谁解决了这个迄今让我们束手无策的唯题,并告知我们,我们将十分感激他.”
实际上,当时欧洲的一流数学家,如约翰.伯努利(Bernoulli J,1667-1748)及其子丹尼尔.伯努利(Bernoulli D,1700-1782)、哥德巴赫(Goldbach C 1690-1764)、莱布尼茨(Leibniz G W,1646-1716)、棣莫佛(Moivre A De,1667-1754)、斯特林(Stirling J,1692-1770)等都未能成功解决这一难题,其中哥德巴赫在与丹尼尔的通信(1729)中给出和的上、下限1.644和1.645;斯特林在其《微分法》中给出近似值
1.644934066.
瑞士大数学家欧拉(Euler L,1707-1783〕最早于1735年解决了这个所谓的“巴塞尔难题”,这是他年轻时期最著名的成果之一.但证明不是很完善,及至后来二重积分及级数的发展,才最终完善了这个极限的证明.
由于π是超越数(林德曼定理),故ζ(2)也是超越数.
再提一个问题:
3.小英爱吃蛋糕, 第一天她独享一只蛋糕,但以后每天来的人按天数的立方递增(即第n天来了n×n×n人),若每天按人数均分蛋糕,问小红累计吃到的披萨会超过一只吗?