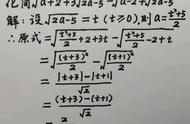前言:为迎接2019年中考,特把初中数学的知识进行梳理,做成了一份很实用的资料,基本囊括了中考所有必考考点,其中有基础知识,也有拔高训练,从前到后、由易到难,希望对学生有所帮助.
此系列前两篇是:《实数相关考点及试题》与《代数式及其求值》,这是第六篇,主要学习二次根式的相关知识.
【考点1】二次根式及其性质
1、概念:一般地,我们把形如√a(a≥0)的式子叫做二次根式.
(1)√a (a≥0)表示a的算术平方根;
(2)a可以是数或式,但a一定要大于等于0;
(3)双重非负性:a≥0,√a≥0.
2、二次根式有意义的条件:被开方数大于等于0.
3、最简二次根式:满足下列三个条件的二次根式,叫做最简二次根式.
(1)被开方数的因数是整数,因式是整式,如2√3,√x(x≥0)是,而√0.5就不是;
(2)被开方数中不含能开得尽方的因数或因式,如√8,√27就不是;
(3)分母不能含有根号,如2/√5就不是.
4、二次根式的性质:

【考点2】二次根式的运算
1、加减运算:二次根式加减时,先将各二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.如:2√3-√27 5√12=2√3-3√3 10√3=(2-3 10)√3=9√3.
2、乘除运算:(1)√a·√b=√ab (a≥0,b≥0);

3、混合运算:二次根式的混合运算顺序与实数的运算顺序相同,有理数的加法交换律、加法结合律、乘法交换律、乘法结合律、乘法的分配律以及多项式的乘法公式,都适用于二次根式的运算.
【考点3】二次根式的估值
(1)先对根式平方;(2)找出平方后所得数字相邻的两个开得尽方的整数;(3)对以上两个整数开方;(4)确定这个根式的值在这两个整数之间.
如对√7进行估值,(√7)^2=7,和7相邻的两个开得尽方的整数是4和9,√4=2,√9=3,则2<√7<3.
注意:要熟记一些常见的二次根式的值,如√2≈1.414,√3≈1.732,√5≈2.236,它们在试题中经常用到.
【考点4】同类二次根式
把几个二次根式化为最简二次根式之后,如果被开方数相同,那么这几个二次根式叫做同类二次根式.
注意:(1)同类二次根式类似于整式的同类项,如5√2和3√2是同类二次根式;
(2)几个同类二次根式在没有化简之前,被开方数可以互不相同,如√0.5,√8,√18都是同类二次根式;
(3)判断两个根式是否是同类二次根式,首先要把它们化成最简二次根式,然后再看被开方数是否相同.
【配套练习】

答案: