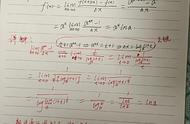对数函数求导公式详细推导,对数函数的导数推导公式

在高等数学中，有许多常用的导数公式，用于计算函数的导数。以下是一些常见的导数公式：

1. 常数法则：如果f(x) = C，其中C是一个常数，则f'(x) = 0。
2. 幂函数法则：如果f(x) = x^n，其中n是一个常数，则f'(x) = nx^(n-1)。
3. 指数函数法则：如果f(x) = a^x，其中a是一个常数且a>0，则f'(x) = a^x * ln(a)。
4. 对数函数法则：如果f(x) = log_a(x)，其中a是一个常数且a>0，则f'(x) = 1 / (x * ln(a))。
5. 三角函数法则：
6. 如果f(x) = sin(x)，则f'(x) = cos(x)。
7. 如果f(x) = cos(x)，则f'(x) = -sin(x)。
8. 如果f(x) = tan(x)，则f'(x) = sec^2(x)。
9. 反三角函数法则：
10. 如果f(x) = arcsin(x)，则f'(x) = 1 / sqrt(1 - x^2)。
11. 如果f(x) = arccos(x)，则f'(x) = -1 / sqrt(1 - x^2)。
12. 如果f(x) = arctan(x)，则f'(x) = 1 / (1 x^2)。
13. 对数导数法则：如果f(x) = ln(x)，则f'(x) = 1 / x。
14. 和、差、积、商的法则：
15. 如果f(x) = g(x) ± h(x)，则f'(x) = g'(x) ± h'(x)。
16. 如果f(x) = g(x) * h(x)，则f'(x) = g'(x) * h(x) g(x) * h'(x)。
17. 如果f(x) = g(x) / h(x)，则f'(x) = (g'(x) * h(x) - g(x) * h'(x)) / (h(x))^2。

这些是高等数学中常用的导数公式，通过熟练掌握这些公式，可以更方便地计算函数的导数。同时，还需要注意特殊函数和复合函数的导数计算，这些公式通常作为基础，并可应用于更复杂的导数问题。