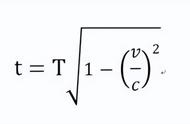现在我们把两个光子钟分开,一个放在地球上,一个放到一艘宇宙飞船上,宇宙飞船相对于地球在做匀速直线运动。

现在地球上的人观察地球上的光子钟,会看到光子在垂直上下振荡,光子上去再回来为1秒,当我们观察处在运动状态的光子钟的时候发现,运动的光子钟中的光子走过的路径不再是垂直上下,而是走出了两条斜线。
这一点很容易理解,如果光子不是再走斜线的话,那光子肯定就跑到光子钟外面去了。从飞船的动图中很容易看到这一点。
如果你理解上以上的所有,也承认爱因斯坦光速不变的假设,那时间膨胀也就显而易见,走斜线的光子钟肯定慢,因为光子速度不变,但是走过的路却长了很多。
当地面上的光子钟振荡完一秒以后,在我们看来飞船上光子钟中的光子还没有振荡完一个来回,因此在地球上的人看来飞船上的时间要比地球上的慢,至于慢多少,这跟飞船相对于地球的速度有关。

利用简单的勾股定理就能很容易地得出,地面上经过的时间tˊ和飞船上的时间t之间的关系。这里就不展开了,直接给出结果。

其中1/√1-v²/c²,为相对论因子,也叫洛伦兹因子,日常生活中,由于v相对于c非常小,所以相对论因子基本上就是1,这样就变成了tˊ=t,退回到了经典的伽利略变换,认为相对运动的观察者时间流逝速度是一样的。
不过当处理高速问题的时候,相对论因子就不能忽略了,在空间中运行的速度越快,时间流逝的速度越慢,如果当速度变为光速的时候,时间流逝就会停止,也就是时间静止。
像光子这样的粒子,在空间中以光速运动,那么时间对于它来说就是静止的,在光子看来,谈论时间没有任何意义,不管多长的时间,都是一眨眼的功夫。
就算是宇宙大爆炸时候诞生的光子到现在,对于光子来说,大爆炸就像刚刚发生一样。遥远星系发出的光子经历漫长的时间和空间来到地球,在我们看来这些光子可能已经几十亿岁了,但是对于光子来说,它的诞生到被接收,只是一瞬间的事。
如果在空间中的运动速度超过光速,很显然相对论因子就会出现一个虚数(负数的平方根),这意味着,这种情况在现实中没有任何物理意义。
这里需要强调的是,超光速并不能让时间倒流,而是没有意义,所以在理论上我们需要禁止超光速的事情发生,至于怎么禁止,爱因斯坦自有妙招,这个我们下节课在说。
下面我们接着说空间收缩,既然我们对时间长短的测量不同,那么我们肯定会对空间长度的测量不同,这一点也很好理解,如果只是时间在变化,距离不变化,就不能保证光速不变这个基本假设了。
那么空间距离如何变化呢?这就要提到洛伦兹变换了,在说洛伦兹变换之前,我们先看看伽利略坐标变换。