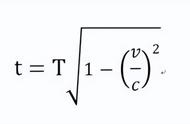现在有一个静止的惯性参照系S系,另外一个参照系Sˊ正在以速度V沿X轴方向运动,那么现在问Sˊ系上的坐标和S系之间满足什么样的数学关系?

没错,这就是伽利略变换,小学生都已经掌握的数学关系。但是这样的数学关系,不再适用光速不变下,以相对论速度运动的物体。
最早,是洛伦兹老先生发现电子的运动不满足伽利略变换,他在1904年的时候,先于爱因斯坦推导出了新的坐标变换公式,称为洛伦兹变换。

从新的坐标变换中,我们看到了刚才推到出来的相对论因子,这也是为什么相对论因子叫洛伦兹因子,因为是洛伦兹最早推出来的。
其中的关于时间变化的公式,跟我们刚才看到的略有不同,原因是刚才时间公式中时间是时长(Δt),也就是两个坐标系相对运动,时长之间的关系,而洛伦兹变化中的时间代表的是坐标轴上的时刻,也就是两个坐标系相对运动,时刻之间的变换关系。
你会发现,当你把两个时刻的变换公式相减的时候,就会得出刚才我们推出来的时长公式。

同样的,我们用洛伦兹变换中关于两个参考系之间坐标的变化公式,也能算出了长度之间关系。
只需要简单的把两个变换出来的两个坐标相减就可以了。