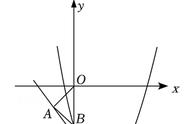
3.如图,在平面直角坐标系 xOy 中,抛物线 y=x2 bx c 与 x 轴交于 A、B 两点,与 y 轴交于点 C,对称轴为直线 x=2,点 A 的坐标为(1,0).
(1)求该抛物线的表达式及顶点坐标;
(2)点 P 为抛物线上一点(不与点 A 重合),联结 PC.当 ∠PCB=∠ACB 时,求点 P 的坐标;
(3)在(2)的条件下,将抛物线沿平行于 y 轴的方向向下平移,平移后的抛物线的顶点为点 D,点 P 的对应点为点 Q,当 OD⊥DQ 时,求抛物线平移的距离.

【解析】
解:
(1)∵ 对称轴为直线 x=2,点 A 的坐标为(1,0),
∴ 点 B 的坐标是(3,0).
将 A(1,0),B(3,0)分别代入 y=x2 bx c,得

则该抛物线解析式是:y=x2﹣4x 3.
由 y=x2﹣4x 3=(x﹣2)2﹣1 知,该抛物线顶点坐标是(2,﹣1);
(2)如图1,过点 P 作 PN⊥x 轴于 N,过点 C 作 CM⊥PN,交 NP 的延长线于点 M,

图1
∵ ∠CON=90°,
∴ 四边形 CONM 是矩形.
∴ ∠CMN=90°,CO=MN,
∵ y=x2﹣4x 3,
∴ C(0,3).
∵ B(3,0),
∴ OB=OC=3.
∵ ∠COB=90°,
∴ ∠OCB=∠BCM=45°.
又 ∵ ∠ACB=∠PCB,( 已知条件 )
∴ ∠OCB﹣∠ACB=∠BCM﹣∠PCB,即 ∠OCA=∠PCM.
∴ tan∠OCA=tan∠PCM.
∴ OA/OC = PM/CM = 1/3.
故设 PM=a,MC=3a,PN=3﹣a.
∴ P(3a,3﹣a),
将其代入抛物线解析式 y=x2﹣4x 3,得(3a)2﹣4(3﹣a) 3=3﹣a.
解得 a1=11/9,a2=0(舍去).
∴ P(11/3,16/9).
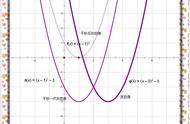
(3)设抛物线平移的距离为 m,得 y=(x﹣2)2﹣1﹣m.
∴ D(2,﹣1﹣m).
如图2,过点 D 作直线 EF∥x 轴,交 y 轴于点 E,交 PQ 延长线于点 F,