二次函数的平移规律是二次函数这一章比较基础的知识点,但是也是必须掌握的知识点。今天我和同学们通过实例详解,掌握二次函数的平移规律,同时掌握它的方法技巧,明白平移的实质是什么。

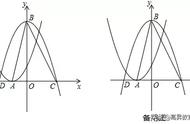
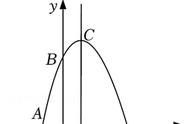
二次函数y=ax² bx c(a≠0)的图象是抛物线,a不仅决定抛物线的开口方向,而且决定抛物线的形状大小(开口大小)。由于抛物线y=ax² bx c(a≠0)通过配方法可转化为y=a(x-h)² k的形式,因此y=a(x-h)² k或y=ax² bx c的图象都可由最基本的二次函数y=ax²(a≠0)通过平移而得到。即:二次函数y=a(x-h)² k(a≠0)的图象是一条抛物线,它的对称轴是直线x=h,顶点坐标为(h,k),是由抛物线y=ax²(a≠0)向右(左)平移lhl个单位长度,再向上(下)平移|k|个单位长度得到的。由y=ax²(a≠0的图象到y=a(x-h)² k(a≠0)的图象具体的平移操作如图下图所示。

涉及抛物线平移的问题时,首先将抛物线解析式化成顶点式,其次根据“左加右减,上加下减”的原则对解析式右侧的代数式进行变形。需要特别注意的是,左加右减是对自变量而言的,上加下减是对解析式整体而言的。对于抛物线的平移问题,关键是正确掌握平移规律,特别注意左右平移的情况,抛物线的平移问题,实质就是平移顶点位置问题,因此化成顶点式是解决问题的前提。

例1:将抛物线y=x²向右平移2个单位长度,再向上平移3个单位长度后,抛物线的解析式为()。
A . y = (x 2 ) ² 3 B.y=(x-2)² 3 C . y = ( x 2 ) ²- 3 D.y=(x-2)²-3
解析:根据函数图像的平移规律,左加右,上加下减。将地物线y=x²向右平移2个单位长度得到抛物线y=(x-2)²,再个向上平移3个单位长度得到抛物线y=(x-2)² 3。因此本题选B.

例2:将抛物线y=x²-4x-4向左平移3个单位长度,再向上平移5个单位长度,得到抛物线的解析式为().
A.y=(x 1)²-13 B.y=(x-5)²-3 C.y=(x-5)²-13 D.y=(x 1)²-3
解析:将抛物线y=x²-4x-4化成顶点式为y=(x-2)²-8,根据平移规律,得y=[(x 3)-2]²-8 5,即y=(x 1)²-3。因此选D。
在学习二次函数平移规律的时候,注意首先转换成顶点式,然后在进行平移。
,