战略上藐视敌人,战术上重视敌人
【题目】
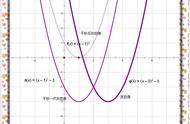
(2018•邵阳)如图所示,将二次函数y=x² 2x 1的图象沿x轴翻折,然后向右平移1个单位,再向上平移4个单位,得到二次函数y=ax² bx c的图象.函数y=x² 2x 1的图象的顶点为点A.函数y=ax² bx c的图象的顶点为点B,和x轴的交点为点C,D(点D位于点C的左侧).
(1)求函数y=ax² bx c的解析式;
(2)从点A,C,D三个点中任取两个点和点B构造三角形,求构造的三角形是等腰三角形的概率;
(3)若点M是线段BC上的动点,点N是△ABC三边上的动点,是否存在以AM为斜边的Rt△AMN,使△AMN的面积为△ABC面积的1/3?若存在,求tan∠MAN的值;若不存在,请说明理由.

【答案】
解:(1)y=x² 2x 1=(x 1)²的图象沿x轴翻折,得y=﹣(x 1)².
把y=﹣(x 1)²向右平移1个单位,再向上平移4个单位,得y=﹣x² 4,
∴所求的函数y=ax² bx c的解析式为y=﹣x² 4;
备注:
(1)平移口诀:上加下减常数项,左加右减自变量;
(2)关于x轴对称,横坐标不变,纵坐标互为相反数。
(2)∵y=x² 2x 1=(x 1)²,
∴A(﹣1,0),
当y=0时,﹣x² 4=0,解得x=±2,则D(﹣2,0),C(2,0);
当x=0时,y=﹣x² 4=4,则B(0,4),
从点A,C,D三个点中任取两个点和点B构造三角形的有:△ACB,△ADB,△CDB,
∵AC=3,AD=1,CD=4,AB=√17,BC=2√5,BD=2√5,
∴△BCD为等腰三角形,
∴构造的三角形是等腰三角形的概率=1/3;
备注:本题特别简单,3选1.
(3)存在.
易得BC的解析是为y=﹣2x 4,S△ABC=1/2AC•OB=1/2×3×4=6,
M点的坐标为(m,﹣2m 4)(0≤m≤2),
①当N点在AC上,如图1,
∴△AMN的面积为△ABC面积的1/3,
∴1/2(m 1)(﹣2m 4)=2,解得m1=0,m2=1,
当m=0时,M点的坐标为(0,4),N(0,0),则AN=1,MN=4,
∴tan∠MAC=MN/AN=4/1=4;
当m=1时,M点的坐标为(1,2),N(1,0),则AN=2,MN=2,
∴tan∠MAC=MN/AN=2/2;

②当N点在BC上,如图2,
BC=√(2² 4²)=2√5,
∵1/2BC•AN=1/2AC•BC,解得AN=(3×4)/(2√5)=(6√5)/5,
∵S△AMN=1/2AN•MN=2,
∴MN=4/AN=(2√5)/3,
∴∠MAC=MN/AN=((2√5)/3)/((6√5)/5)=5/9;

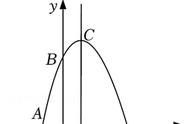
③当N点在AB上,如图3,作AH⊥BC于H,设AN=t,则BN=√17﹣t,
由②得AH=(6√5)/5,则BH=√((√17 )²-((6√5)/5 )² )=(7√5)/5,
∵∠NBG=∠HBA,
∴△BNM∽△BHA,
∴MN/AH=BN/BH,即MN/((6√5)/5)=(√17-t)/((7√5)/5),
∴MN=(6√17-6t)/7,
∵1/2AN•MN=2,
即1/2•(√17﹣t)•(6√17-6t)/7=2,
整理得3t2﹣3√17t 14=0,△=(﹣3√17)²﹣4×3×14=﹣15<0,方程没有实数解,
∴点N在AB上不符合条件,
综上所述,tan∠MAN的值为1或4或5/9.
备注:本题看似复杂,实际比较简单。因此在做题的时候,一定要从心理上面战胜恐惧。
由于AM为斜边,当点N分别在AB和AC上时,可以先定N,过点N作AN的垂线交BC于点M即可。当点N也在BC上时∠ANM为90°,则只需过点A作BC的垂线即可确定点N,点M的位置是任意的。
设未知数表示出△AMN的面积令其等于△ABC的1/3即可。