二次函数一般形式平移规律总结,二次函数一般式平移规律

（1）具体步骤：

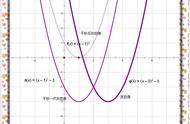
先利用配方法把二次函数化成y=a(x-h)² k的形式，确定其顶点(h,k)，然后做出二次函数y=ax²的图像，将抛物线y=ax²平移，使其顶点平移到(h,k).具体平移方法如图所示：

（2）平移规律：在原有函数的基础上“上加下减，左加右减”.

二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达

1. 关于x轴对称

y=ax² bx c关于x轴对称后，得到的解析式是y=-ax²-bx-c；

y=a(x-h)² k关于x轴对称后，得到的解析式是y=-a(x-h)²-k；

2. 关于y轴对称

y=ax² bx c关于y轴对称后，得到的解析式是y=ax²-bx c；

y=a(x-h)² k关于y轴对称后，得到的解析式是y=a(x h)² k；

3. 关于原点对称

y=ax² bx c关于原点对称后，得到的解析式是y=-ax² bx-c；

y=a(x-h)² k关于原点对称后，得到的解析式是y=-a(x h)²-k；

4. 关于顶点对称

y=ax² bx c关于顶点对称后，得到的解析式是y=-ax²-bx c-b²/2a；

y=a(x-h)² k关于顶点对称后，得到的解析式是y=-a(x-h)² k．

5. 关于点(m,n)对称

y=a(x-h)² k关于点(m,n)对称后，得到的解析式是y=-a(x h-2m)² 2n-k

根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此│a│永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．

例题解析：

例1：

解答：

例2：