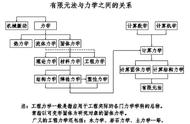
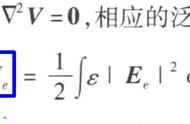有限元方法(FEM)是一种数值技术,用于对任何给定的物理现象进行有限元分析(FEA)。
必须使用数学来全面理解和量化任何物理现象,例如结构或流体行为,热传输,波传播和生物细胞的生长。其中大多数过程都是使用偏微分方程(PDE)进行描述的。但是,对于用于解决这些PDE的计算机,在过去的几十年中已经开发了数值技术,而当今最杰出的技术之一就是有限元法。

首先,了解不同类型的偏微分方程及其在有限元中的适用性是非常重要的。理解这一点对每个人来说都是特别重要的,不管使用的动机是什么。有限元分析。重要的是要记住,FEM是一个工具,任何工具只有它的用户好。

图01:环空上的拉普拉斯方程。图像四十二[CC by-SA3.0(https://creativecommons.org/licenses/by-sa/3.0)],通过维基共享。
PDE可分为椭圆型、双曲型和抛物线型。在求解这些微分方程时,需要提供边界和/或初始条件。根据PDE的类型,可以评估必要的输入。每一类PDE的例子包括Poisson方程(椭圆型)、波动方程(双曲型)和Fourier定律(抛物型)。
求解椭圆型偏微分方程的方法主要有两种:有限差分法(FDM)和变分法(或能量法)。有限元法属于第二类。变分方法主要是基于能量最小化的哲学。
双曲型偏微分方程通常与解决方案的跳跃有关。例如,波动方程是双曲PDE。由于解中存在间断(或跳跃),原有限元技术(或Bubnov-Galerkin法)不适合求解双曲型偏微分方程。然而,多年来,为了扩大有限元技术的适用性,人们对有限元技术进行了改进。
在结束这一讨论之前,有必要考虑使用不适合于PDE类型的数值框架的后果。这样的使用会导致被称为“不恰当定位”的解决方案。这可能意味着域参数的微小变化会导致解的大振荡,或者解只存在于域或时间的某一部分,这是不可靠的。适定性解释被定义为对定义的数据持续存在唯一解决方案的解释。因此,考虑到可靠性,获得良好的解是非常重要的.
有限元法能量最小化原理有限元是如何工作的?主要的驱动力是什么?能量最小化原理是有限元法的主要支柱。换句话说,当一个特定的边界条件被应用到一个物体上时,这可能导致几种配置,但实际上只有一种特定的配置是可能的或实现的。即使在多次进行仿真时,也会获得相同的结果。为什么会这样?

图02:虚拟工作原理的描述
这是遵循能量最小化原则的。它指出,当施加边界条件(如位移或力)时,在物体可以采取的众多可能配置中,只有总能量最小的配置才是所选择的配置。
有限元法有限元法的历史从技术上讲,根据一个人的观点,有限元可以说起源于欧拉的作品,早在16世纪。然而,最早的关于有限元的数学论文可以在Schellback[1851]和Courant[1943]的著作中找到。
有限元法是由工程师独立开发的,用于解决与航空航天和土木工程有关的结构力学问题。这些发展始于20世纪50年代中期,分别发表了特纳、克劳夫、马丁和托普[1956]、阿吉里斯[1957]和巴布斯卡(Babuska)和阿齐兹(Aziz)[1972]的论文。Zienkiewicz[1971]、Strang和Fix[1973]的著作也为有限元的未来发展奠定了基础。
对这些历史发展的有趣回顾载于Oden[1991]。
弱形式有限元的第一步是识别与物理现象相关的PDE。PDE(或微分形式)称为强形式,积分形式称为弱形式。考虑简单的PDE,如下所示。该方程由两边的试函数v(X)相乘,并与区域[0,1]积分。