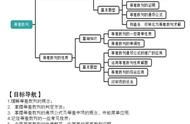
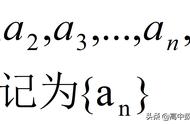一、有关数列的概念:
1、数列是按照一定顺序排列的一列数,数列中的每一个数叫做这个数列的项。
数列中的每一项都和它的序号有关,排在第一位的数称为这个数列的第 1 项 (通常也叫做首项),排在第二位的数称为这个数列的第 2 项 , ...... ,排在第 n 位的数称为这个数列的第 n 项 。
2、数列的一般形式可以写成如下形式:

数列一般形式图(1)
3、项数有限的数列叫做有穷数列,项数无限的数列叫做无穷数列。
4、如果数列 {an} 的第 n 项与序号 n 之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式 。
5、从数列中的第二项起,每一项都大于前一项的数列叫做递增数列;
从数列中的第二项起,每一项都小于前一项的数列叫做递减数列;
各项相等的数列叫常数列;
从第二项起,有些项大于它前一项,有些项小于它前一项的数列叫做摆动数列 。
6、数列的图像都是一群孤立的点 。
7、数列有三种表示形式:列举法、通项公式法、图像法 。
8、递推公式:如果已知数列 {an} 的第 1 项 (或前几项),且任一项 an 与它的前一项 an-1 (或前 n 项)间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的递推公式。递推公式也是给出数列的一种方法 。

二、数列通项公式的常用求法
1、根据数列的某几项写出数列的通项公式,常用到 “观察法”,具备较强的观察和逻辑推理能力是解决这类题目的关键。
例1:根据数列的前 4 项,写出它的一个通项公式:
(1)9,99,999,9999,…

例题1图(1)