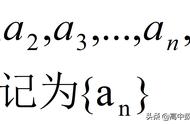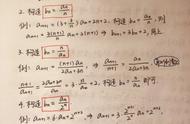科学也跨界,它总以意想不到的方式,无处不在。
看似呆板的数列中能呈现出炫彩的科学美感。不信?那就和中国科学院物理研究所曹则贤老师一起来了解下斐波那契数列的神奇幻化吧!

自然数是无穷多的。如果把一些数字按规律排成一排,就构成了一个数列。用函数表示就是数列 {an}。
如:偶数 2,4,6,8……
奇数 1,3,5,7……
三角数 1,3,6,10,15……
素数(原子) 2,3,5,7,11,13,17……
将数列的项依次用加号连接起来的函数就是级数。由傅里叶级数 (Fourier series)发展的傅里叶分析技术是最有力的数学、物理工具。别不相信,展开成本征函数级数就是量子力学的基本操作。

人类历史中,意大利数学家斐波那契(Leonardo Fibonacci)是一个天才,年少时随着父亲在北非做生意,学习了阿拉伯数字。1202年,他撰写了《Liber Abaci(算书)》一书,向西方传播印度-阿拉伯的数字系统。
阿拉伯数字体系让数学、物理学成为可能。数学、物理是就用阿拉伯数列、拉丁 希腊字母表示的,这是所有想要从事科学研究的人都必须掌握的一套话语体系!
在《Liber Abaci(算书)》一书中,斐波那契提出了一个有趣的问题:有一对成年兔子,每隔一个月就生一对小兔子,而小兔子一个月后也成年了加入生小兔子的行列,如果每对兔子都经历这样的出生、成熟、生育的过程,并且永远不死,问N个月后有多少对兔子?我们不妨用树状图展示一下:

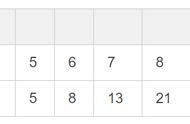
用数列表示为:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…,数列中的每一项都被称为斐波那契数,用符号Fn表示。F(0)=1,F(1)=1, F(n)=F(n - 1) F(n - 2)(n ≥ 2,n ∈ N)。
这就是著名的斐波那契数列(Fibonacci数列),也叫做“兔子数列”。
虽然很有意思,但是,就这?斐波那契数列对人类发展有什么意义?
每一个数学、物理对象后面都有太多我们不知道、或者知道了也理解不了的内容。我们理解不了,科学家们却能理解。
在数学中,杨辉三角形是出现在概率论、组合学和代数中的二项式系数的三角形数组。斐波那契数列与杨辉三角形(即,帕斯卡三角形)有关联:杨辉三角形中的对角线之和,是斐波那契数,如图所示。