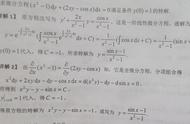本文简述用scipy工具包求解微分方程的基本方法。.
导入必要的工具包:
import matplotlib.pyplot as plt
import scipy as sp
from scipy.integrate import odeint例1:一阶微分方程的解法(如图1)
物体下落时,空气摩擦力的方程如下:

空气摩擦力表达式的自定义函数:
def dvdt(v, t):
return 3*v**2 - 5
v0 = 0
解法如下:
t = np.linspace(0, 1, 100)
sol = odeint(dvdt, v0, t)
v_sol = sol.T[0]
v_sol
v_sol的结果如图2:

绘制出微分方程的解集图,如图3:
plt.plot(t, v_sol)


图4中文字及方程的输入形态,如下:
**二阶ODE方程**
钟摆方程如下:
$$\theta'' - \sin(\theta) = 0$$
Scipy只能用来解一阶ODE方程,但是所有的任何二阶ODE都可以转换为两个一阶ODE方程。同理,更高阶的ODE方程也可转换为多个一阶ODE方程来解。
设 $\omega = d\theta/dt$,那么可以推导出以下的ODE方程:
$$d \omega / dt = \sin(\theta)$$
$$d \theta / dt = \omega $$
设 $S = (\theta, \omega)$
例4中表达式的自定义函数及其初始值:
def dSdt(S, t):
theta, omega = S
return [omega,
np.sin(theta)]
theta0 = np.pi/4
omega0 = 0
S0 = (theta0, omega0)
求解代码如下:
t = np.linspace(0, 20, 100)
sol = odeint(dSdt, S0, t)
theta, omega = sol.T
求解结果如图5:
plt.plot(t, theta)
plt.show()