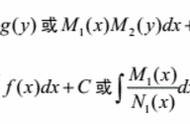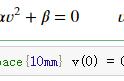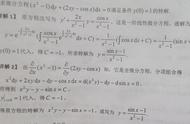如何证明微分方程,微分方程的解怎么判断

微分方程是在高等数学里经常遇到的一种方程，相比我们在初高中学到的简单方程，这种方程有着非常神秘的性质。那么为什么这种方程如此神奇，为什么会需要这种独特的方程呢？虽然我只是一个学渣，但是还是愿意过来谈谈自己的想法。

方程是什么？方程实际上就是一种含有未知数的等式。通过建立未知数和已知数之间的关系我们可以对方程进行求解。用天平来比喻，就是在等式的两边放上各种各样的砝码，有些砝码的重量我们知道，有些我们不知道，而通过天平的平衡我们可以知道这些位置砝码的重量。

△用天平来比喻方程△

当然，有些时候方程不是要求到具体的未知数的值，而是要算到不同的未知数之间的关系，保证我们知道了某几个未知数之后就可以知道最后那个未知数。比如说下图就是x、y、z三个未知数之间的关系式，当我们知道了x和y的值之后，自然也就知道了z的值了。

△多元方程的图像△

而微分方程同样是为了求解未知数、已知数之间的关系，但是未知数不再只是以自己本身的面貌出现，而是以未知数导数的形式出现。所以我们在微分方程里面不仅仅会看到未知数y，还会看到未知数相对于其他未知数之间的导数关系，比如说dy/dx，比如说∂y/∂x，等等。

△微分方程包含了未知数的导数△

比如说，我们用一个方程描述一辆汽车在一条笔直的公路上的运动，如果这个方程中只有距离x这一个目标未知数，那么这就不是一个微分方程，比如说x=10*t，其中t是时间，通过这个方程我们直接知道了目标未知数的表达式；

但是如果一个方程中既有路程x，又有路程的变化率（也就是速度），那么方程就变成了微分方程，比如说我们把方程写成了dx/dt=10，其中t是时间，那么这个方程我们建立的方程中就包含了路程变化率跟已知量之间的关系。

我们先不去说纯数学里的微分方程，只说在物理中经常会用到的微分方程。而之所以我们会在物理中那么经常地用到微分方程，本质上是因为人类掌握的往往都是物体的局部规律，所以需要微分方程来描述这种局部规律，然后由局部规律反推整个物体的性质。

比如说一个复杂的物体，我们要知道其中应力是怎么分布的，那么我们很难找到一个直接表达式来描述应力在各个点上的值，但是我们却可以知道某一个点上的物理量变化规律。因为一个点是没有形状的，性质是确定的。

△复杂物体上的应力分布△

因此，我们写下的方程不是一个描述整个物体应力分布的方程，而是物体局部性质的方程。这个方程对于这个物体内部的每一个点都是适用的，所以我们建立起来的是每个点的平衡关系。在科学概念里面，我们往往为了表述方便，把这个点描述成所谓的“微元体”。

△微元体上的受力平衡关系△

但是，如果只是把一个物体分割成无数个彼此不相关的微元体，那么这样的分割就完全没有意义，所以我们不仅要描述这个微元体上局部的性质，还要建立起来微元体与周围微元体之间的关系。所以这个时候物理量的导数就有必要了，因为导数本质就是“变化率”，描述的就是一个点与周围点之间的关系。

所以说，我们建立起来的微分方程实际上是描述物体内部各个点的性质，并且通过这个微分方程把这些点联系起来，织成一张“大网”，最后反推整个物体的性质。

简单说，微分方程的意义就是描述物体局部物理量还有这些物理量的变化规律的，通过求解微分方程我们可以架起物体局部和整体之间的桥梁。比如说，下面一张图就是复杂的N-S方程，用来分析复杂流体的性质。

△复杂的N-S方程△

虽然公式这么长，但是实际上描述的也是流体之中一个点的性质而已。一团每个点都满足这个方程、流体的边缘还满足特定条件的流体，就是我们最终会求解的流体。