n条直线相交最多的交点数是多少,n条直线相交的交点规律

很多时候，当孩子碰到一道没有做过的数学题时，不会立刻就想到解法。那么，遇到未知问题时，该如何解决呢？

小学阶段，抽象能力（包括从物体到数的抽象和从数到符号的抽象）以及类比与归纳推理能力是要着重培养的能力。关于这一点，可参考我之前的文章《深度好文：小学数学应该学什么，怎么学？》。

有些人喜欢夸夸其谈地讲大道理，但就数学而言，缺乏具体案例来讲道理难免会让大道理成为无源之水。我更喜欢把道理融入到具体的案例中。下面就通过一个例子及其拓展来展示如何发展这些能力。

下面这道题是我做过的经典问题之一：

n条直线最多把平面分成多少部分？

如果没有做过这个问题，那绝大部分人的第一反应会是从最简单的开始尝试。这就非常好。探索和尝试本来就是最可贵的解题品质。

观察上面的规律，1，2，4，7，11，后面一个应该是16。

大部分学生到这里都可以总结出具体的结论，如：第10条直线在第9条直线的基础上可以多分出10块，第100条直线可以在第99条直线的基础上多分出100块。

我们的工作是要引导孩子撇开具体的数，进而完成从10或100这些具体的数到符号n的抽象，这也是是小学阶段要培养的主要能力之一。

一般化地，n条直线最多把平面分成的块数为n-1条直线最多把平面分成的块数加n。

有了上面的结论，可以进一步推导出n条直线共把平面分为：

验算一下：当n=1,2,3时，分别为2，4，7，满足。

（注：在刚开始尝试符号抽象的时候，孩子经常会犯一些错误，这时候用具体值代入验算能确保及早发现并纠正错误。）

解题到这当然不算结束，核心问题还没有解决。

我们刚才的归纳只是一种猜测。归纳有可能正确，有可能错误。为此，我们还需要证明刚才归纳的正确性。为什么n条直线最多分的块数是在n-1条直线最多分的块数基础上加n呢？这就涉及到“直线-交点-线段-平面”之间的关系。

我们知道，如果一条直线上有n个点，那么这些点将把这条直线分成n 1段。

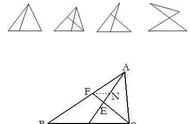
原来有n-1条直线，加上第n条直线后，这第n条直线最多与之前的n-1条直线有n-1个交点，这些交点将把第n条直线分成n段。而每一段都将把原来的一个区域一分为二，因此多出了n块。下图给出了n=3的示意图。

如果是应试，这个问题就结束了。但如果是平时，我们还得多想一点。如果不是直线，而是封闭的圆形，那么会如何？这就是常说的举一反三能力。比如下面的问题：

n个圆，最多把平面分成多少部分？

同样，我们可以从小规模开始尝试并归纳。

很多人据此就开始归纳：每多一个圆，最多将平面分成的块数将比之前翻倍。

但如果继续画4个圆，就发现怎么都分不出16块。4个圆，我们只能最多分出如下图所示的14个区域。所以，归纳是经验的总结，但有的时候并不一定正确。为了获得正确的归纳，我们不要吝啬自己的劳动，要有尽可能多的样本才行。

因此，我们得到了1，2，4，8，14这个序列。猜测一下，后面应该是22才对。

推理的过程，则可以类比直线分平面的做法。如果在n-1个圆的基础上增加一个圆，那这个圆最多与前面的n-1个圆有2(n-1)个交点（如上图所示，第4个红色圆加上去后，最多与前面的3个圆都相交，一共有6个红色的交点），这2(n-1)个交点把第n个圆分成2(n-1)段（注：封闭图形），每一段都把原来的一块一分为二，因此最多多分出2(n-1)块。

据此，n个圆最多将平面分成:

1 1 2 4 … 2(n-1)=2 n(n-1) (n≥1)

所以，这类问题的关键是看有几个交点。继续拓展一下，如果把圆换成三角形，又如何呢？

n个三角形最多把平面分成多少个部分？

有了前面直线分平面和圆分平面的做法，我们可以进行类比，考虑下面的问题：两个三角形最多有多少个交点？答案是6个。

一般化地，如果是在n-1个三角形的基础上再增加1个三角形，那这个三角形和之前的n-1个三角形最多可以有6(n-1)个交点，可以把第n个三角形分成6(n-1)段，因此多分出6(n-1)块。

当然，还可以对上面的图形进行组合，生成更复杂的问题，比如：

1个三角形，3个圆最多可以把平面分成多少部分？

这个问题，如果试图去画图，会比较吃力，很少有人能在没有理论指导的前提下画正确。尝试一下就知道，要让三角形与每个圆都有6个交点，这并不容易。

但这并不妨碍我们进行理论分析。理论上，先画3个圆，最多把平面分成8部分，然后再加1个三角形，这个三角形与每个圆最多有6个交点，总共最多有18个交点，这些交点将把这个三角形分成18段，因此多分出18块，总共8 18=26块。具体如下图。