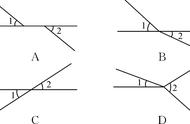
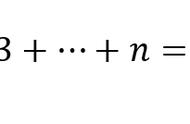平面上有n条直线两两相交,但没有三条直线交于一点。问这n条直线把平面划分成多少个区域?
分析:当我们遇到一个较为复杂的数学问题时,往往想起与它类似的问题,类似的形式,类似的解法等等,并联想起与它相应的定理,相应的公式,相应的法则等,从而把所遇到的问题与联想起的问题进行比较。通过类比推理的思考方法,将所遇到的问题进行等效"转化",向想起的问题"靠拢",又将联想起的类似的方法"移植"到所遇到的问题上。因此在解决直线分平面的问题时,我们可通过类比和联想,从点分直线的情况出发来探索直线分平面的问题。

解:首先我们来考虑点分直线的问题。设一直线上的n个点能将直线分成an个部分,那么容易得到an=n 1。
接着我们再来研究直线分平面问题。平面上有n条直线,其中任何两条不平行,任何三条不共点,设这n条直线将平面分成bn个部分,在观察的基础上进行归纳可知,第k+1条直线与前k条直线均相交得k个交点,由前面点分直线的情形可知,该直线被k个交点分成k+1段,而其中每一段都把平面上的每一个区域分成两个区域,所以平面部分应增加(k+1)块。由此可得递推关系式为

所以,当k=1时,b₂-b₁=2,
当k=2时,b₃-b₂=3,
当k=3时,b₄-b₃=4,
…
当k=n-1时,bn-bn-1=n,
把以上n-1个式子相加得:
(b₂-b₁)+(b₃-b₂) (b₄-b₃)+…+(bn-bn-1)
=2+3+4+…+n,
则: bn-b₁=2+3+4+…+n,
即:bn=2+2+3+4+…+n。

因此n条两两相交,且没有三线交于一点的直线可把平面分成