n条直线相交最多的交点数是多少,n条直线相交的交点规律

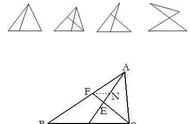
上面这个过程也给我们提出了一个新问题：理论和试验操作，你该相信哪个？

当我们还没有一个正确的理论作为支撑时，应该用尽可能多的试验来归纳总结出更具普适意义的理论。而当我们证明了某个理论的正确性后，就应该用普适的理论来指导具体的试验操作。

更复杂一点的问题，可以把直线、圆和三角形混合起来，比如这样的问题：

在一个无限大、无边界的平面上画1条直线，可以把平面分成2部分；在平面上画1个三角形，也可以把平面分成2部分。那么，在平面上画1个三角形、2个圆和2条直线，最多可以将平面分成几部分？

我们还是按照老思路。

第一步：2个圆把平面分成4块。

第二步：加1个三角形，与前面两个圆最多有12个交点，这12个交点将把三角形分成12段，因此多分出12块，最多分成16块。

第三步：再加1条直线，与两个圆和一个三角形可以最多分别有2个交点，共6个交点，这6个交点将这条直线分为7段，因此可以多分出7块，因此最多分成16 7=23块。

第四步：最后再加1条直线，与两个圆和一个三角形可以最多分别有2个交点，与之前的直线最多有1个交点，最多共7个交点，这7个交点将这条直线分成8段，因此可以多分出8块，最多分成23 8=31块。

当然，我们也可以从直线开始：

第一步：2条直线最多把平面分成4部分。

第二步：加1个圆，与两条直线最多有4个交点，这4个交点将圆分成4段，多分出4块，因此最多分成4 4=8块。

第三步：再加1个圆，与两个直线最多有4个交点，与前一个圆最多有2个交点，因此最多有6个交点，这6个交点将圆分成6段，从而可以多分出6块，因此最多分成8 6=14块。

第四步：再加1个三角形，与前面的两个圆最多有12个交点，与两条直线最多有4个交点，一共最多有16个交点，这16个交点把三角形分成16段，多分出16块，因此最多分成14 16=30.

咦，两种做法，一个最多分成31块，一个最多分成30块，怎么结果不一样呢？为什么顺序不一样，结果竟然不同呢?

同一个问题当然不可能出现两个不同的结果，必有一个的分析出了问题！

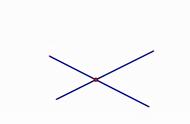
问题其实出在这里。如果我们先放圆，这时把平面分成了2部分，再加1条直线，虽然2个交点把直线分成了3段，但圆外的两段并没有多分出两块，而是只分出1块！如下图所示。

而如果像下图这样一端不出去，那么实际上左边的这段开口红色线段并没有把外部的区域一分为二。这实际上是拓扑的特点。

反过来，如果先放一条直线把平面分成2部分，再放上一个圆，那么圆被分成2段，每一段都把原来的区域一分为二了。

因此，上述问题的正确答案应该是30，而不是31。

有了这些以后，如果把这个问题二维拓展到三维，即从平面拓展到空间呢？（注：这个问题对小学有点超纲，更适合中学生）

n个平面最多把空间分成多少部分？

这个问题，我们也可以从头开始尝试。

如果就此归纳出4个平面最多可以把空间分成16部分，那就又错了。有孩子用豆腐或橡皮泥切了半天，发现怎么切都切不成16块，最多只能切15块。

那怎么思考这个问题呢？如果我们从点分直线成线段、线段分平面成区域这一思想衍生过来，那我们就会发现这个平面分空间问题的求解思路也可以类比直线分平面的做法。

在直线分平面的问题中，我们通过多出的线段来分析增加一条直线后多分出的平面数；那在平面分空间的问题中，我们是不是也可以通过多出的平面来分析增加一个平面后多分出的空间数呢？

在3个平面的基础上增加1个平面，那么前面3个平面最多和这个平面有3条交线，这三条交线将把这第4个平面最多分成7部分（由直线分平面的结论得到），每一个部分将把原来所在的空间一分为二，因此在8块的基础上多分出了7块，也就是说4个平面最多把空间分为8 7=15部分。

当然，抽象能力、类比和归纳推理的能力的培养，肯定不是一蹴而就的，需要长期把上面这种方法融入到实践中，更需要给孩子足够的时间去思考和拓展一个问题。

作者简介：昍(xuan)爸，中科院计算机博士，现为211大学计算机专业教授。曾获初中和高中全国数学奥林匹克联赛一等奖，江苏赛区第一名，高考数学满分。平时注重在生活中引导孩子进行数学思考，著有《给孩子的数学思维课》一书，开设有公众号xuanbamath。