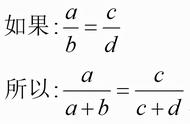拉普拉斯变换(拉氏变换)是一种解线性微分方程的简便运算方法,是分析研究线性动态系统的有力数学工具。简单点说,我们可以使用它去解线性微分方程,而控制工程中的大多数动态系统可由线性微分方程去描述,因此拉氏变换是控制工程领域必不可少的基础。
什么是拉氏变换呢?首先,我们来看一下拉氏变换的定义——
设时间函数为f(t),t>0,则f(t)的拉普拉斯变换定义为:

其中,f(t)称为原函数,F(s)称为象函数。
一个函数可以进行拉氏变换的充要条件为:
(1)在t<0时,f(t)=0;
(2)在t≥0的任一有限区间内,f(t)是分段连续的;
(3)当t→﹢∞时,f(t)的增长速度不超过某一指数函数,即:

接下来为大家介绍几种常见的时间常数拉氏变换,大家在看下面几种时间常数拉氏变换的时候可将几个时间常数与这三个条件一一对应,有助于理解记忆。
单位脉冲函数数学表达式为: