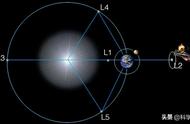
地日L4和L5点虽然是最好的天然稳定平衡点,但因距离地球较远,以现阶段科技难以有效利用。除去2010TK7小行星及可能的其他小行星或星云外,并无任何人造物体在L4和L5点。
而地日系统中没有利用价值的只有L3点,这距离地球最远的拉格朗日点,恰好位于地球公转轨道另一端的L3点被太阳完全阻挡,因而无法观测和通讯。外加上天然的不稳定平衡,所以并不存在利用价值。
而地月系统的拉格朗日点虽然L1- L3是不稳定的,但可选取适当的初始扰动,使相应平动点附近的运动仍为周期运动或拟周期运动。即选取这样的初始扰动使系统原来的解退化为周期解,相应的运动变为稳定的,此时这种稳定称为条件稳定。

像L1位于地球和月球连线上,距离月球6.5万公里,可以理解为月球引力和地球引力相互抵消的点,该处的飞行器无法在水平位置保持自平衡,稍受扰动就会偏向其中一方,不过即使是不稳定平衡,借助控制系统也能使飞船的平衡转为稳定,所以处在该点的物体可以选择在地球和月球引力的共同作用下,可以几乎不消耗燃料而保持与月球同步绕地球做圆周运动。据此,科学家设想在L1点建立空间站。

在高达0079的宇宙纪元里,所有的太空殖民空间站均位于地月L点宇域
而L2位于月球背面一侧,距离月球6.5万公里,该处附近的飞行器无法保持自平衡,飞行器需要围绕L2点绕行,从而达到动态平衡;所以中国鹊桥号的终点站就是环绕地月拉格朗日2点的使命轨道。
这样,地月引力将达到平衡,鹊桥号相对地球和月球达到静止状态,轨道维持需要的燃料少,获取的日照充足,可以说选择L2点是中国能够发射成功全球首颗月球中继信号卫星的创新之举。

L3:位于地球背向月球一侧,比月球轨道(38万公里)稍微小一点,该处的飞行器无法保持自平衡。利用价值比较小。
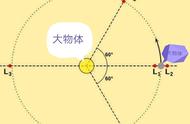
L4、L5:对称的两个点,每个点与地球、月球都构成等边三角形,这两个拉格朗日点属于自平衡点,该处的飞行器就算受到一定的扰动,也能主动回到平衡点,有科学家提出了在在地月系统拉格朗日点L(4,5)建立空间VLBI的设想。