小学数学《鸡兔同笼》教案
一、教学目标
【知识与技能】
了解”鸡兔同笼”问题,感受中国古代数学问题的趣味性。
理解掌握并会运用列表法、假设法、算术法、方程等不同方式解决“鸡兔同笼”问题。
【过程与方法】
“鸡兔同笼”最早出现在《孙子算经》里,学习“鸡兔同笼”可以培养学生逻辑推理能力,让学生体会代数方法的一般性。
经历自主探索解决问题的过程,体验解决问题的策略的多样化;在解决问题的过程中,提高逻辑推理能力,增强应用意识和实践能力。
【情感态度价值观】
感受中国古代数学问题的趣味性。
二、教学重难点
【教学重点】
掌握运用列表法、假设法解决“鸡兔同笼”问题。
【教学难点】
理解掌握假设法,能运用假设法解决数学问题。
三、教学过程
(一)引入新课
PPT呈现课本的主题图,并提问:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?是什么意思?大家能不能算出各几何呢?
引出课题——《鸡兔同笼》
(二)探索新知
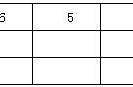
先从简单问题出发,呈现例1:8个头,26只脚,鸡和兔子各几只?猜测一下
教师总结学生回答:3只兔子,5只鸡,22只脚;4只兔子,4只鸡,24只脚。均不对
追问:按顺序列表填写一下,应该是各有几只?
得出结论有3只鸡,5只兔子。
进一步追问:还有没有其他方法?
学生活动:前后六人一小组讨论。
教师总结:假设笼子里都是鸡,那么多出来的脚的个数除以2便是兔子的只数,用头数减去便得到鸡的只数。如果假设所有的动物都是鸡,那么就有8×2=16只脚,这样就多出26-16=10只脚。多出的10只脚均为兔子的,一只兔子比一只鸡多2只脚,所以算得有10÷2=5只兔,3只鸡。
(三)课堂练习
教师出示导入中的问题“上有三十五头,下有九十四足,问雉兔各几何”
学生活动:学生自主选择喜欢的方法进行解决,一名学生到黑板上板演,其余学生独立完成,在黑板上板演的学生在结束后充当小老师给其他同学进行讲解
(四)小结作业
提问:今天有什么收获?
教师引导学生回顾解决鸡兔同笼问题的方法。
课后作业:思考还有没有其他方式能够解决鸡兔同笼问题?自己设计鸡兔同笼的问题去考考小伙伴或家人。
例:有鸡兔共35只,脚94只,求鸡兔各几只?
假设法
1、假设笼子中全是鸡:
因为共有35个头,则鸡的脚数为2×35=70(只),
这样,鸡的脚数比总脚数少94-70=24(只),
而一只兔子比一只鸡多的脚数为4-2=2(只),
故少了的24只脚可用兔子来增加,可得
兔子的只数为24÷2=12 (只),
鸡的只数为35-12=23(只)。
2、假设笼子中全是兔子:
因为共有35个头,则兔的脚数为4×35=140(只),
这样,兔的脚数比总脚数多140-94=46(只),
而一只鸡比一只兔子少的脚数为4-2=2(只),
故多了的46只脚可用鸡来减少,可得
鸡的只数为46÷2=23(只),
兔子的只数为35-23=12(只)。
抬脚法
解法:
兔的只数=(总脚数-总头数×鸡的脚数)÷(兔的脚数-鸡的脚数)
鸡的只数=总头数-兔的只数
让鸡和兔同时抬起2只脚,这时笼子里只剩下兔子的脚,剩下兔子的脚数为
“总脚数-总头数×2” 剩下的脚数除以2就是兔子的只数
兔的只数=(94-35×2)÷2=12(只)
鸡的只数=35-12=23(只)
,