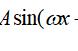一、说教材
(一)教材的地位和作用
本节内容在全书及章节的地位:《数列(第一课时)》是高中数学新教材北师大版必修五第 1章第一节。
本节内容在全书及章节的作用:数列是在紧接着学习函数之后的内容,它在教材中起着承前启后的作用,一方面,可以加深学生对函数概念的认识,使他们了解不仅可以有自变量连续变化的函数,还可以有自变量离散变化的函数;另一方面,又可以从函数的观点出发变动地、直观地研究数列的一些问题,以便对数列性质的认识更深入一步。数列还有着非常广泛的实际应用;数列还是培养学生数学能力的良好题材。所以说数列是高中数学重要内容之一。
学情分析:学生已经掌握了函数的有关对应的知识和概念,同时已经具备了一定的自学能力,多数同学对数学的学习有相当的兴趣和积极性,但在探究问题的能力,合作交流的意识等方面发展不够均衡,尚有待加强。
(二) 教学目标的确定
根据上述教材结构与内容分析,以及学情的分析,制定如下教学目标:
1、 基础知识目标:形成并掌握数列的概念,理解数列的通项公式。并通过数列与函数的比较加深对数列的认识。
2、 能力训练目标:培养学生观察、归纳、类比、 联想等发现规律的一般方法。
3、 情感目标: 让学生在民主、和谐的共同活动中感受学习的乐趣。
4、 教学重点、难点、关键的确定
本着新课程标准,在吃透教材基础上,我觉得本节课是本章内容的第一节课,是学生学习本章的基础,为了本章后面知识的学习,首先必须掌握数列的概念,其次数列的通项公式是研究后面等差数列、等比数列的灵魂,所以本节重点确定如下:
教学重点: 数列概念及其通项公式
由特殊到一般,由现象到本质,要求学生从一个数列的前几项或相邻的几项来观察、归纳、类比、联想出数列的通项公式,学生必须通过自己的努力寻找出数列的通项与项数n之间的关系来,对学生的能力要求比较高,所以本节难点确定如下:
教学难点:建立数列的通项公式
教学关键:就是教会学生克服难点,办法是让学生学会观察数列的前几项的特点,在观察 和比较中揭示数列的变化规律。
二、说教法
数学是一门培养和发展人的思维的重要学科,因此,在教学中,不仅要使学生“知其然”而且要使学生“知其所以然”。为了体现以学生发展为本,遵循学生的认知规律,体现循序渐进与启发式的数学教学原则,我进行了这样的教法设计:在教师的引导下,创设问题情景,通过开放性问题的设置来启发学生思考,在思考中体会数学概念形成过程中所蕴涵的数学方法,使之获得内心感受。
三.说学法
我以建构主义理论为指导,从学情出发,采用着重于学生探索研究的启发式教学方法,结合师生共同讨论、归纳总结。在课堂结构上,我根据学生的认知水平,设计了 ①创设情境——引入概念②观察归纳——形成概念③讨论研究——深化概念④即时训练—巩固新知⑤总结反思——提高认识⑥任务后延——自主探究六个层次的学法,它们环环相扣,层层深入,从而顺利完成教学目标。
四、说教学程序
环节 | 知识产生和发展 过程的教学设计 | 双 边 活 动 | 设 计 意 图 |
一.实例导入 | 1.讲述“棋盘上的麦粒”历史典故 | 师生共同演绎,推导得出每个格子里的麦粒数按放置的先后排成一列数: | 创设情景-引入概念 用古老的有关国际象棋的传说引入,符合高一学生喜欢探究新奇奥妙事物的特点。有利于激发学生的学习兴趣。 |
2.观察下列数: (1)2,3,4,5,6,7, (2)1984年到2004年我国体育健儿参加六次奥运会获得的金牌数排成一列数: 15,5,16,16,28,32 (4)1,0.1,0.01,0.001 … (5)-1,1,-1,1,-1,1… (6)2,2,2,2,2,2… | 师生共同观察,归纳总结所举例子得出共同特点: 它们是有一定顺序的一列数 | 观察归纳——形成概念 通过设计了各种类别的数列,引导学生概括总结出本课新的知识点:数列的定义及其有关概念。并且这些实例贯穿本节所有知识点的讲解应用中。 | |
二. 探 索研究发现规律 | 例1 项 2 3 4 5 6 7 序号 1 2 3 4 5 6 教师引导: 观察这列数的每一项与与它的序号是否有一定的关系? 学生归纳: 这里的每一项都是它相应的序号加1,可用公式: 引导学生得出结论:如果数列{ }的第n项与n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式 | 观察归纳——形成概念 让学生在观察归纳等活动中得数列通项的定义。同时也有效的发展了学生的推理能力,引导学生感受数学的思想方法。从而体验学习成功的乐趣,也使师生关系由原来的教与学的关系变成了亲密的合作伙伴。 | |
环节 | 知识产生和发展过程 | 设 计 意 图 |
二. 探 索 研 究 发 现 规 律 | 2.再看实例(5)这列数的每一项和它相应的序号可用公式: 还可以用公式: 引导学生得出结论:同一数列通项可以不唯一 再如实例中(2)题,问学生:年份和这年得到的金牌总数可以用公式来表示吗? 生答:项和项数的对应关系存在,但不能用公式表示 再次引导学生得出结论:有的数列可以没有通项, 最后告诉学生: 我们以后要研究的是有通项的数列 | 讨论研究——深化概念 师生共同观察 这两个实例得出了课本中没有的对数列通项的更深层的理解 , 不但加深了学生对数列通项概念的理解,多层次、多角度展开对概念的剖析,更增强了学生探究的好奇心,激发出潜在的创造力,逐步形成创新意识 |
3.数列与函数的关系: 对于有通项的数列,如 实例(1)题,每一项的序号与它对应的序号有着一一对应的关系,引导学生联想到函数,从函数观点看数列,可以看作是一个定义域为正整数集(或它的有限子集)的函数当自变量从小到大依次取值时对应的一列函数值,而数列的通项公式也就是相应函数的解析式 引导学生总结: 数列是特殊定义域的函数 进而提问: 数列可以用图像来表示吗? 生答:可以,由于定义域不连续,因此图像也不连续,是一群孤立的点。如下图所示: 33 | 讨论研究——深化概念 引导学生观察对比,层层深入,揭示说明概念的内在联系,让所有学生都在开放的教学过程中探索发现规律,获取知识 | |
4.数列的分类: 回到实例中, 引导学生按项数分类: 按增减性分类: 按有界无界分类: 除此之外还有常数列等 | 讨论研究——深化概念 用数列 的分类引领学生理解分类思想方法 |
环节 | 知识产生和发展过程 | 设 计 意 图 |
三 例题讲解 | 例1 根据数列 的通项公式,写出前5 项: (1) (2) 例2 在数列 –1, 0, 中, 0.08是它的第几项? 例3 写出下面数列的一个通项公式: (1) 1,3, 5, 7, 9… (2) 4,8, 16, 32, 64… (3) | 即时训练—巩固新知 例1 ,例2 是对基本概念的训练和巩固,而例3的设计由浅入深,层层深入,其中(1)(2)是(3)(4)铺垫和引导的题,其中第(4)题是学生的易错题,这样设计重在分散难点来突破重点,让学生初步掌握求数列通项的方法,体现循序渐进的教学法则 |
(6)3, 8, 15, 24, 35, … (8) 0.9, 0.99, 0.999… | 即时训练—巩固新知 这4道题的设计原则也是环环相扣,但较之前4题难度拔高了,意在培养学生探究问题的能力,提升思维的层次,本节课的难点也就随之突破. | |
四 小结 | 可由小组推荐他们的一位组员作总结性发言, 谈谈他们一组在学习中遇到的问题以及本节课所要掌握的知识等等。 | 总结反思——提高认识 学生小结能发挥学生的主体作用,逐步提高学生的表达能力和自我获取知识的能力 |
五 作 业 布 置 | (1)阅读作业:课本P6-8 (2)书面作业:课本P8 习题1 的 1,2题 (3)弹性作业: 递增数列1,3,7,11,13,17,19,...包含所有既不能被2整除,又不能被3整除的正整数,求此数列的第100项。 | 任务后延——自主探究 作业分为三种形式,体现作业的巩固性和发展性原则.阅读作业中的问题思考是后续课堂的铺垫,而弹性作业不作统一要求,供学有余力的同学课后研究.同时,它也是新课标里研究性学习的一部分. |
五、 教学评价
本节课,采用“探究发现式”教学模式为学生创设了的探究知识的情景,从而充分调动学生学习数学知识的积极性,使学生有自主发现知识、创造性地解决问题的时间、空间。在整个的设计过程中,始终体现以学生为中心的教育理念。在学生已有的认知基础上进行设问和引导,关注学生的认知过程,强调学生的品德、思维和心理等方面的发展。重视讨论、交流和合作,重视探究问题的习惯的培养和养成。同时,考虑不同学生的个性差异和发展层次,使不同的学生都有发展,体现因材施教的原则。
六、 板书设计:
§1数 列 | ||
1.概念: | 2、例题1 (学生板书) 例题2 例题3 | 3、练习 4.小结 |