01 电荷及其量子性
电荷是自然界中粒子的一种基本属性。电荷有两种,分别称为正电荷和负电荷。自然界的粒子所带的电荷不能无限小,一个基本的电荷量是指电子所带的电量,数量为 ,物体所带电荷必定是基本电荷的整数倍,这是电荷的量子性。
根据电荷间作用的规律,即“同种电荷相互排斥,异种电荷相互吸引”,可以确定电荷的种类是两种。电荷是粒子的属性,同质量一样,电荷也具有相对论不变性,不同的是,它还满足电荷守恒定律。
02 点电荷
点电荷是指大小和形状可以忽略,可以看成一个点的带电体。同质点一样,是否能被看作点电荷,也依具体问题而定。
03 库仑定律
同种电荷相互排斥,异种电荷相互吸引。真空中,两个点电荷之间的相互作用力沿着二者连线的方向,按照如下公式给出 其中, 是点电荷的距离, 是从施力电荷指向受力电荷的单位矢量, 是真空的电容率。
理解库伦定律矢量式的含义,当考虑电荷1对电荷2的作用时, 从1指向2,否则 就反向。无论电荷1和2的电性如何,只要规定正电荷用正数,负电荷用负数,库仑力的方向总能自动通过矢量式获得。
04 试验电荷
为了尽量减少因为电场力过大,而导致场源电荷重新分布,进而影响空间电场的分布,基于点电荷的模型,定义所谓“试验电荷”,即带电量足够小的点电荷。
05 电场与电场强度
与超距作用观点不同,场的观点认为作用是通过场有限速度来传递的。电场就是传递电荷相互作用的媒介。
试验电荷在空间某点所受到的电场力与试验电荷的量的比值描述该点的电场的强弱,称之为电场强度,其方向与该点正电荷受力方向一致,即
06 电场的叠加原理
根据力的叠加性可知,空间任一点的电场是周围所有电荷在此贡献电场的矢量和,此即为电场的叠加原理。
07 点电荷的电场强度
一个点电荷 在离它距离为 的点激发的电场强度为
其中 是指从点电荷 指向该点的单位矢量。
基于此,由点电荷组成的带电体系的电场就可以根据电场强度的叠加来获得。
离散的点电荷体系的电场为 电荷连续分布的带电体系的电场为 微元电荷 的具体形式依赖于带电体的维度,当电荷分别为线、面和体分布时, 分别为 , 和 。
这是计算电场强度的第一种方法。
08 电场线及电场通量
电场线:一种描述电场强度矢量分布的模型,它在某处的切线方向对应该点的电场的方向,在某点垂直于电场的单位面积内,穿过的电场线的条数 为该处电场强度的大小 ,即
电场线起始于正电荷或无穷远,终止于负电荷或无穷远。电场线永不相交,不会在没有电荷的地方中断。

电通量:根据以上电场线的模型易知 如果要知道空间中一个面内 有多少根电场线穿过,只要对此式积分即可。由于电场线本身并不存在,而是一种假想模型,因此说“条数”是不合适的,而是用通量来描述,叫做电通量,用 表示,即 电通量的符号取决于面积矢量与电场强度的方向的夹角,如果夹角是锐角,则通量为正,否则,通量为负。
规定闭合曲面的法线方向以向外为正,向内为负。因此,若电场线从曲面内射出,则通量为正,否则通量为负。
09 高斯定理
真空中,穿过任意闭合曲面的电场强度的通量 ,等于该曲面内所包含的电荷的代数和 除以 ,即 高斯定理表明,电荷是电场的源,电场是有源场。
关于高斯定理要注意:
a. 闭合曲面外的电荷对整个曲面上的电通量没有贡献,曲面上的的电通量全部由内部的电荷贡献。
b. 高斯定理描述的是曲面的通量与内部的电荷之间的关系,并不是描述曲面上的电场与电荷之间的关系。
c. 高斯面上的电场并非只由曲面内的电荷贡献,而是由空间所有电荷共同贡献的。
d. 作为一个数学定理,高斯定理是普遍成立的,对曲面的形状没有任何要求,但是只有当电场分布具有某种对称性时,高斯定理才能为我们所用——用来求空间电场的分布。
当电场分布具有高度对称时,例如球形带电体,圆柱形带电体,无限大带电平面等,电场强度可从积分符号中提出,因而可据此求解电场强度。这是求解电场强度的第二种方法。
10 典型静电场案例
a. 电荷线密度为 的无限长直线,其方向沿试验电荷与线电荷垂线b. 电荷面密度为 的无限大平面 ,其方向沿着过试验电荷与电荷面垂线方向c. 电荷线密度为 ,截面半径为 的无限长圆柱面 d. 半径为 的均匀带电球面 e. 半径为 的均匀带电球体 另外,若电荷的分布只与径向距离有关,则上述规律中的 的部分依然成立。
11 静电场的环路定理
静电场的电场强度沿任意闭合路径的积分必为零,即 这表明静电场力做功与路径无关,静电场力是保守力。
12 电势能与电势
电势能:电荷 在电场中移动时,电场力所做的功只与始末位置有关,与路径无关,这说明存在一个函数,它在始末点的函数值的差对应电场力所做的功,因此引入电势能函数 ,它满足 若选择 为零势能参考点,则 点的电势能函数就被确定下来了零势能参考点:零势能参考点的选择是任意的,一般选择无穷远点。因此上式通常写作 但当带电体本身延伸到无穷远处时,不能选择无穷远点为零势能参考点。
电势:单位正电荷在某点的电势能的值,即
电势与电场强度一样,描述的是电场本身的性质,与试验电荷无关。这是电势的定义,也是计算电势的第一种方法。
电势差:空间两点之间的电势相减得到的就是两点之间的电势差,即
电场力做功:电场力做功等于电荷乘以电势的减少值,即
13 电势的叠加原理
电场中任一点的电势等于各个点电荷单独存在时对该点形成的电势的代数和,即
14 点电荷的电势
点电荷 对离它距离为 的点产生的电势为 据此可得到带电体系在空间形成的电势。其中,离散的点电荷系的电势为
电荷连续分布的带电体系的电势为 这是计算电势的第二种方法。
15 电场强度与电势的关系
电势是电场强度的积分,但是反过来,如何通过电势得到电场强度呢?
电势 的全微分为 根据矢量的点乘,上式也可以写为 上式即为 ,以无穷远处为电势零点,则任意点 的电势为 而电势的定义为 比较上述两式即得
因此电场强度是电势的负梯度,电场强度与电势之间是积分和微分的关系。在直角坐标系中表示为 这是计算电场强度的第三种方法。
等势面:电势相等的点构成的面。一般,电场中相邻等势面的电势差为一常量。这样就导致电场大的地方,等势面较密集,电场小的地方,等势面较稀疏。
等势面与电场线:电场线是从电势高的等势面指向电势低的等势面,等势面与电场线处处正交。
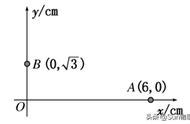
电势为零的点,电场不一定为零,例子:等量异号电荷连线中点。
电场为零的点,电势不一定为零,例子:等量同号电荷连线中点。
The End

本文原文已群发,此为方便即时更新的版本。

*Zealandia_the_8th
扫码关注,收获更多干货!
西藏点地梅,高山上的小仙女。
视频 | 傅里叶变换的工作原理系列(第十部分):结语
视频 | 傅里叶变换的工作原理系列(第九部分):卷积 II
视频 | 傅里叶变换的工作原理系列(第九部分):卷积 I
视频 | 傅里叶变换的工作原理系列(第八部分):复数
复数及复变函数动画解析
视频 | 傅里叶变换的工作原理系列(第七部分):欧拉公式与欧拉恒等式
视频 | 傅里叶变换的工作原理系列(第六部分):相位
视频 | 傅里叶变换的工作原理系列(第五部分):什么是声音?
视频 | 傅里叶变换的工作原理系列(第四部分):傅里叶级数的诞生
视频 | 傅里叶变换的工作原理系列(第三部分):傅里叶与拿破仑
视频 | 傅里叶变换的工作原理系列(第二部分):傅里叶本人的前半生
视频 | 傅里叶变换的工作原理系列(第一部分):导言