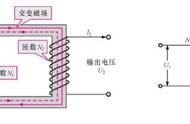
▲图24-4
如图24-4所示为某无分支直流磁路,磁通沿磁性材料形成闭合路径,此时有无分支磁路的欧姆定律如图所示。
其中磁动势F为电流I与线圈匝数N的乘积,单位为安培(A)或安培匝数(AT)。∑Rm为磁路的总磁阻,单位为每亨利(1/H)。磁动势类似于电路中的电动势,是磁通源(励磁电流)。由于铁磁材料的磁导率μ不是常数,即磁性材料的磁阻不是常数,所以图24-4中的磁路欧姆定律只能对磁路进行定性分析。
直流磁路中的磁通不变,励磁线圈中没有感应电动势,励磁电流I仅由励磁线圈的外加电压U和线圈电阻R决定(I=U/R)。励磁线圈的电阻是不变的,外加电压一定时,若磁路状况(中心长度、截面、材料)不同,则总磁阻和磁通也不同。
交流磁路:在由交流电流励磁的磁路中,磁通随时间不断交变,这样的磁路称为交流磁路。其中交流磁路的励磁线圈称为交流铁芯线圈。交流磁路中由于磁场方向的不断改变,导致磁通不断变化,这会导致铁磁材料产生磁滞损耗和涡流损耗。关于磁滞损耗和涡流损耗,其实在之前的学习中我有提到过,就是不知道大家是否还记得。
涡流:当磁路中的磁通交变时,会在铁芯中感应出涡旋状的电流,称为涡流。涡流使铁芯发热并消耗能量,称为涡流损失(涡流损耗)。在交流磁路中,铁芯中产生磁滞损失和涡流损失的总和称为铁芯损失,简称铁损。

▲图24-5
如图24-5所示,我们以硅钢片制成的铁芯为例,硅钢叠片处于交变磁通中,根据电磁感应定律与右手螺旋定则,每一片硅钢片中都会产生感应电动势,该电动势会形成一圈一圈的涡流,又由于硅钢片有电阻的存在,所以有能量的损失,这就是涡流损失。
知道了磁路是怎么一回事后,我们继续学习磁路的基本定律。
2、安培环路定律(全电流定律)我在之前的学习分享中也提到过安培环路定律,当时没有以此展开讲解,现在是时候让大家知道它到底指什么了。

▲图24-6
如图24-6所示,无限长直载流导线的磁感线是在垂直于导线的平面内以导线为中心的一组同心圆,电流方向不同的导线所产生的磁感应线环绕方向不同,这些方向不同的磁感应线在某一点会进行矢量叠加。
任取一闭合磁感应线,沿磁感应线(磁通)绕行方向,把磁感应线进行微分,然后任取一线元dl,与该处的磁场强度H进行积分,所得的结果就是该闭合磁感应线所包围的电流的代数和。
安培环路定律电路正负方向的规定:任意选定一个闭合回线的围绕方向,凡是电流方向与闭合回线围绕方向之间符合右手螺旋定则的电流为正,反之为负。
安培环路定律把电流和磁场强度联系起来,另外,若是在均匀磁场中,根据安培环路定律,我们可以很快得出Hl=NI,(或H=NI/l)。
3、磁路的欧姆定律若某磁路的磁通为φ,磁通势(磁动势)为F,磁阻为Rm,则φ=F/Rm,这就是磁路的欧姆定律。在上文就有提到,磁路里的磁通就好比电路里的电流,电路里的欧姆定律为I=U/R,显然和磁路里的欧姆定理极为相似。
虽然磁路和电路很相似,但是它们之间的区别也有很多,所以磁路分析的特点和电路分析并不相同。磁路分析的特点主要有以下几点:
(1)在处理电路时不涉及电场问题,在处理磁路时离不开磁场的概念;
(2)在处理电路时一般可以不考虑漏电流,在处理磁路时一般都要考虑漏磁通;
(3)磁路欧姆定律和电路欧姆定律只是形式上相似。由于μ不是常数,其随励磁电流而变,磁路欧姆定律不能直接用来计算,只能用于定性分析;
(4)在电路中,当E=0时,I=0;但在磁路中,由于有剩磁,当F=0时,φ不为0。
4、磁路基尔霍夫定律(1)、基尔霍夫磁通定律:有分支磁路如图24-7所示,指任取一闭合面,根据磁通连续性原理,进入闭合面的磁通,必等于流出闭合面的磁通,即穿过闭合面的磁通的代数和为零(∑φ=0),此称为基尔霍夫磁通定律。

▲图24-7
回顾之前所学的电路基尔霍夫电流定律,即电路中任一个节点上,在任意时刻,流入该节点的电流之和等于流出该节点的电流之和(∑I=0),我们可以发现,磁路基尔霍夫磁通定律与电路基尔霍夫电流定律极为相似。
就如那句歌词“吃了我的给我吐出来”,不管是闭合平面或者是空间闭合曲面,进入该闭合面的磁通总是等于流出该闭合面的磁通。
(2)、基尔霍夫磁压定律:指磁路中沿任意闭合曲线磁位差的代数和等于沿该曲线磁动势的代数和,即∑NI ∑Hl ∑Um=0。
在上文中就提到过,磁路的磁动势F为电流I与线圈匝数N的乘积,即F=NI。类似于电路中的电动势,由于励磁电流是线圈产生磁通的来源,故称NI为磁路的磁动势F。类似于电路中的电压,磁路中也有磁压的概念,即磁场强度与磁路平均长度的乘积,称为磁压,用符号Um表示,Um=Hl。
如图24-8所示的磁路,磁路可能由多种尺寸、多种材料构成,有的还含有气隙。结合磁动势F的定义与上文的全电流定律Hl=NI,此时有NI=∑Hl,推广到任意磁路中,显然也有∑NI ∑Hl ∑Um=0,这就是基尔霍夫磁压定律。