矩阵探索者联盟
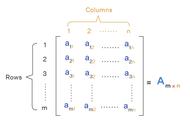
矩阵在线性代数中扮演着中心角色,它们是组织和表示线性方程组、线性变换以及向量空间的强大工具。具体而言,矩阵的作用可以从以下几个方面来理解:
1. 线性变换的表示:矩阵提供了一种方式来表示在线性空间中的变换,比如旋转、缩放、反射等。一个矩阵乘以一个向量相当于对这个向量施加一个线性变换。
2. 线性方程组的解法:对于一组线性方程,矩阵可以用来构建一个系数矩阵,通过求解这个矩阵所对应的线性系统,可以找到方程的解或者判断解的存在性。
3. 向量空间的描述:矩阵可以用来描述向量空间的内积、正交性以及维度等属性。特别是,方阵的特征值和特征向量可以揭示向量空间的结构特性。
4. 线性系统的状态空间分析:在控制理论和系统工程中,矩阵用于表示系统的状态空间模型,帮助分析和设计系统的动态行为。
5. 数值分析和计算:在数值线性代数中,矩阵运算(如矩阵分解和迭代方法)是解决大规模线性系统问题和求解特征值问题的基础。
6. 图像处理和计算机图形学:在这些领域中,矩阵用于图像的变换、滤波和增强,以及在三维图形中表示对象的旋转和位移。
7. 统计学和机器学习:在统计模型和机器学习算法中,矩阵用于数据的组织、处理和分析,如主成分分析(PCA)和各种优化问题。
综上所述,矩阵不仅在理论上构成了线性代数的骨架,而且在实际应用中也发挥着至关重要的作用,是连接数学理论与现实世界的桥梁。